Bridge scour, Victor M. Ponce

BRIDGE SCOUR

Victor M. Ponce

181125

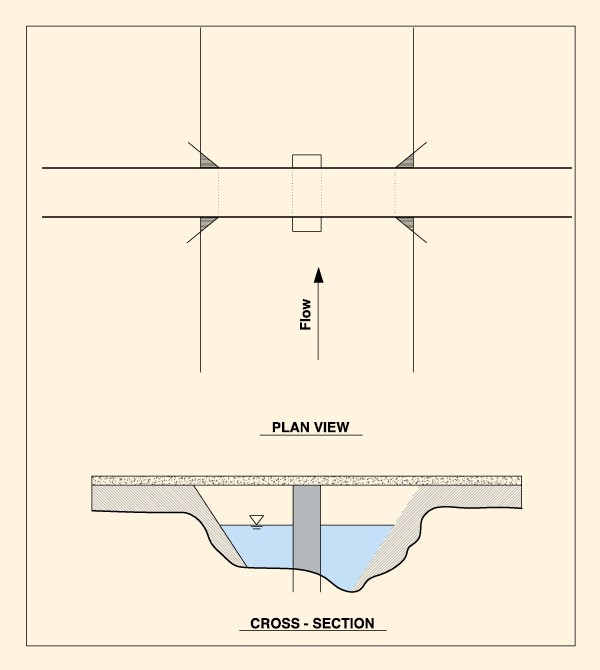
1. BRIDGE SCOUR

Bridges are road structures designed to make it possible to cross a river or stream. Bridges differ from culverts in their shape and in that they are usually much larger (Fig. 1). Generally, bridges are justified in cases of road crossings with major rivers, or when the great volume of vehicular traffic requires it. In many cases, the abutments and/or piers of the bridge are placed directly on the bed of the streams or rivers (Fig. 2), which forces the need for a stability analysis.

Fig. 1 Bridge over the Sado river, Alcaçer do Sal, Portugal.

Fig. 2 Bridge over the Kings river, near Stratford, California.

The stability analysis includes the study of scour of one or more piers and/or abutments of a bridge crossing. During the passage of a flood, the flow is forced to go under the bridge. The presence of one or more abutments reduces the effective cross section of the flow; therefore, the velocities increase and with this, the sediment discharge. This process eventually leads to the undermining (erosion) of the soil around the pier, which, if of sufficient magnitude, can endanger the stability of the superstructure and lead to the eventual failure of the bridge.

Scour is a transient flow phenomenon which occurs during the passage of a flood. The process is dual, characterized by: (1) erosion during the rise of the flood hydrograph, and (2) deposition during the recession. In many cases, the hole produced by the erosion during the ascent is filled by the deposition during the recession. The failure occurs when the depth of the hole, called the depth of scour, is of such a magnitude that it compromises the lower level of the foundation of the structure. Therefore, the objective of the analysis is to determine the depth of scour that enables the design of the bridge foundation (in type, size and depth) with an adequate safety factor.

2. TYPES OF CHANNEL DEGRADATION, SCOUR, OR EROSION

Scour, degradation, or erosion in the vicinity of a bridge structure may be due to one or more of the following processes:

General scour: The relatively slow degradation of the fluvial bed, which obeys to transient phenomena of sediment transport in the stream or river, acting in the longitudinal macroscale, beyond the immediate vicinity of the bridge;
Contraction scour: The erosion of the natural cross section of a river, caused by contraction (i.e., reduction of flow area) imposed by the presence of the piers or abutments;
Local scour: The rapid erosion of the fluvial bed, during a flood event, around the piers or abutments;
Lateral migration: The change of alignment of a river, which leaves the bridge effectively outside the established course prior to migration.

General scour is caused by a reduction in the supply of sediments in sections located upstream of the point of interest. Generally this is due to the degradation immediately downstream of a dam, caused by the phenomenon of "hungry water" (Fig. 3), or to excessive extraction of aggregates from the neighboring river beds (Fig. 4). In some cases, the reduction in the supply of sediments may be due to natural or artificial changes in the runoff coefficient of the basin located upstream.

degradacion debajo de la presa Fort Sumner

Fig. 3 Degradation below Fort Sumner dam, Pecos river, New México (Lane, 1955).

Fig. 4 General degradation due to sand mining, Guadalupe Creek, Baja California, Mexico.

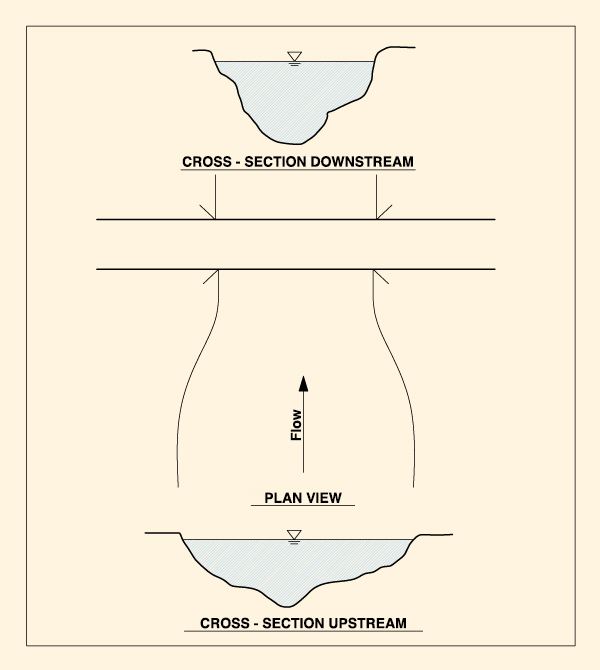
Contraction scour usually manifests itself throughout the width of the river, during the passage of an extraordinary flood (Fig. 5).

Fig. 5 Bridge over the Cuiaba river, Mato Grosso, Brazil, during the flood of January 10, 1995.

Local scour is produced by the removal of soil material around the piers, abutments, and other bridge foundation structures, caused by the acceleration of the flow in the neighborhood and the formation of vortices induced by flow obstructions. Figure 6 shows the failure of a railroad bridge near Kingman, Arizona, on August 9, 1997. The bridge failure, which led to the derailment of the train, was due to erosion and scouring of the piers and foundations of the bridge, as a result of a flood of 50-year return period (National Transportation Safety Board, 1998).

Fig. 6 Failure by local scour underneath railroad bridge No. 504.18, naer Kingman, Arizona.

Lateral migration occurs when a river carries excessive amounts of sediment in relatively flat geomorphological situations, which forces it to fill its channel and, consequently, to look for new courses, usually during the passage of an extraordinary flood (Fig. 7). In general, any widening or lateral displacement of a fluvial channel endangers the operability of a bridge placed on it (Fig. 8). There does not seem to be a simple solution to this bridge design problem.

Fig. 7 (a) Satellite image showing the changes in course of the Kosi river, in Bihar, India.

Fig. 7 (b) Changes of course, in the past three centuries, of the Kosi river, in Bihar, India.

Fig. 8 Abandoned railroad bridge over the Pirai river, Santa Cruz, Bolivia.

3. CONTRACTION SCOUR

Contraction scour occurs when the flow area of a stream is reduced either: (a) by a natural contraction, or (b) by an artificial contraction due to the presence of a bridge. In most cases, contraction scour results in the deepening of the riverbed. A deeper channel will always have a greater velocity.

Figure 9 shows the Pongo de Manseriche, a natural contraction sculpted in rock, through which the Marañón River, one of the two great rivers that eventually form the Amazon River, reduces its width to 35 m as it descends the Eastern Andes Ranges, in Amazonas, Peru. The passage through the pongo is particularly dangerous because of the eddies that form due to the extreme contraction of the flow, as observed in the video Pongo de Manseriche.

Carlos Correa Loyola

Fig. 9 Minimum section at the Pongo de Manseriche, on the Marañon river, Amazonas, Perú.

In rivers with a predominantly sandy bed, there are two types of contraction scour: (1) under clear water, and (2) under a live bed. Scouring by clear water occurs for low Froude numbers, that is, when the average velocity is less than the critical velocity necessary for the start of bed movement. In this case, the flow area in the section of the bridge, during the flood, increases until the average velocity becomes equal to the critical velocity for bed movement.

Live bed scouring occurs for higher Froude numbers, for which the average velocity is greater than the critical velocity necessary for the start of bed movement. In this case, the flow area in the section of the bridge, during the flood, increases until the amount of transported material leaving the control volume is equal to that which is entering.

The existing formulas for contraction scour require the determination of the type of scour. To determine if the flow immediately upstream of the bridge is producing bed movement, it is necessary to calculate the critical velocity. For this purpose, the following formula may be used:

V_c = K_u y^1/6 D₅₀^1/3

(1)

in which:

V_c = critical velocity necessary for the start of bed sediment movement, in m/sec or ft/sec;

y = flow depth immediately upstream of the bridge, in m or ft;

D₅₀ = average diameter of sediment particles in the streambed, located immediately upstream of the bridge, in m or ft; and

K_u = empirical constant, equal to 6.19 in the SI (metric) system, and 11.17 in the U.S. customary system of units.

To obtain the D₅₀ of the bed material, it must be sampled in the first 0.3 m depth. Equation 1 is applicable to granular materials, being restricted to values of D₅₀ ≥ 0.0002 m (0.2 mm). For smaller sizes, cohesion has the effect of increasing the critical velocity.

3.1 Design geometry

The analysis of contraction scour depends on the particular geometrical conditions of the design. The following cases may arise:

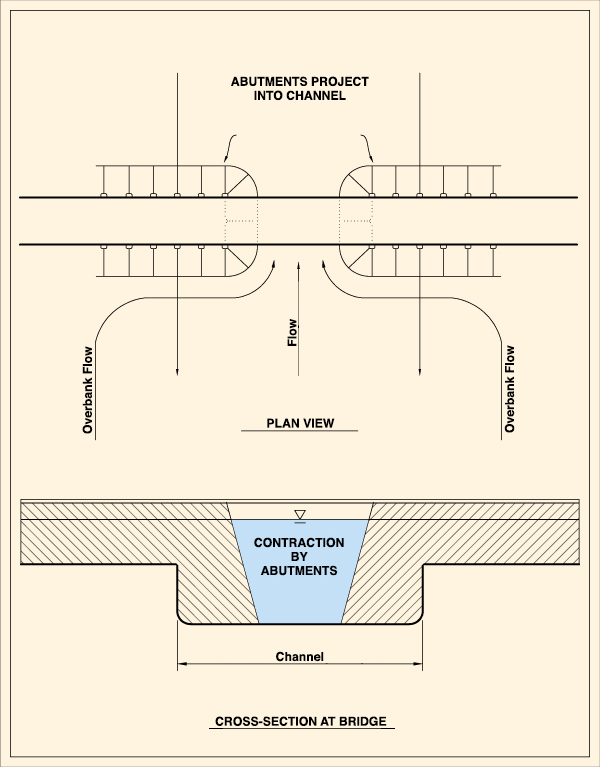
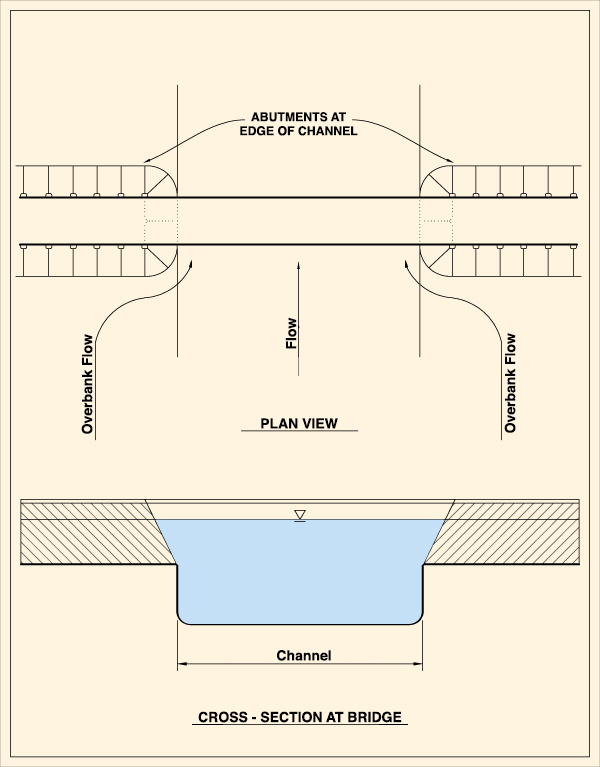
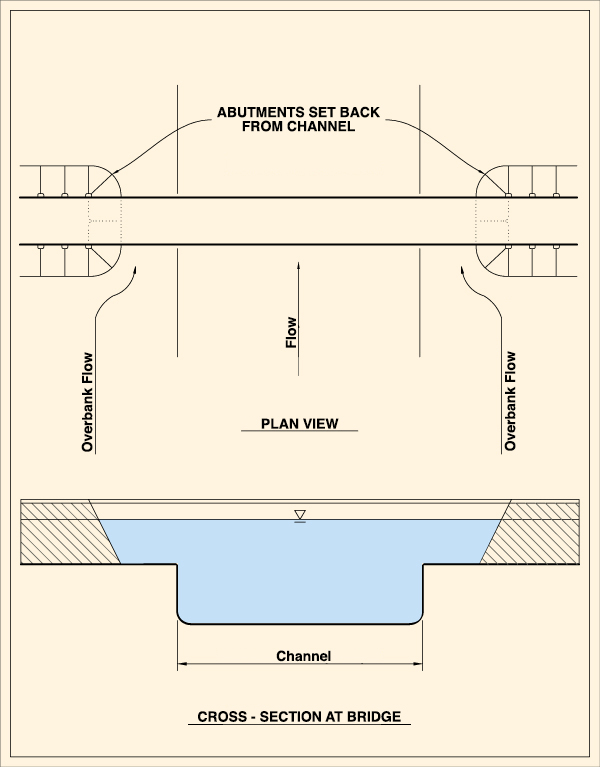
1. With flow in the flood plain, the distance between the abutments is (Fig. 10):

Lesser than the width of the main channel.
Equal to the width of the main channel.
Greater than the width of the main channel..

Fig. 10 (a) Contraction scour: Case 1a.

Fig. 10 (b) Contraction scour: Case 1b.

Fig. 10 (c) Contraction scour: Case 1c.

2. Without flow in the flood plain, the section of the stream is (Fig. 95):

Naturally narrower in the bridge and/or the section immediately downstream.
Artificially narrower on the bridge due to obstruction caused by piers and/or abutments.

Fig. 11 (a) Contraction scour: Case 2a.

Fig. 11 (b) Contraction scour: Case 2b.

3.2 Contraction under live bed

The contraction scour under live bed conditions is calculated using the modified Laursen equation (1960):

y_s Q₂ W₁ y_o
^_____ = (^____) ^0.86 (^____) ^k₁ - ^____
y₁ Q₁ W₂ y₁
(2)

in which:

y_s = mean depth of contraction scour under live bed, in m or ft;

y_o = average depth of flow under the bridge, before scouring, in m or ft;

y₁ = mean depth immediately upstream of the bridge, in m or ft;

Q₁ = flow in the upstream section of the bridge, which transports sediment from the bed, comprising only the flow in the main channel, in m³/s or ft³/s;

Q₂ = flow in the contracted section, in m³/s or ft³/s;

W₁ = bottom width in the upstream section of the bridge, which transports sediment from the bed, in m or ft;

W₂ = bottom width in the contracted section, which transports sediment from the bed, in m or ft;

k₁ = exponent shown in Table 1, in which:

V_{_{_*}} = shear velocity immediately upstream of the bridge = (gy₁S₁)^1/2 ;

S₁ = slope of the energy line in the main channel; and

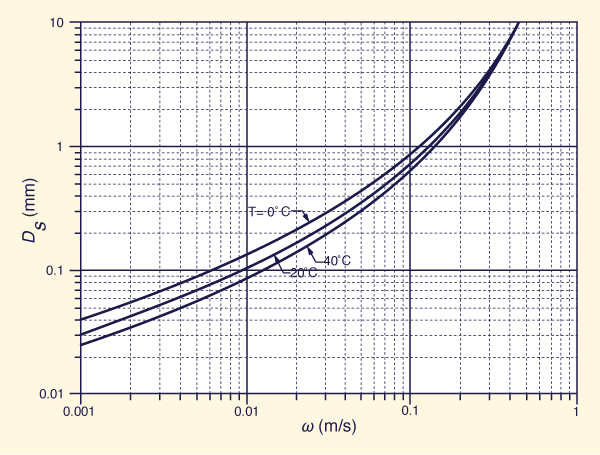
ω = fall velocity of the sediment, a function of the grain diameter D_s (Fig. 12), that is, the mean grain diameter D₅₀.

Table 1 Exponent k₁ in Eq. 2.
Ratio *V_{_{_}} / ω**	Mode of transport of the sediment load	k₁
< 0.5	Predominantly bedload	0.59
0.5 - 2.0	Both bedload and suspended load	0.64
> 2.0	Predominatly suspended load	0.69

Fig. 12 Fall velocity of a sediment particle.

With reference to Eq. 2, we note the following:

For cases 1a and 1b, the value of W₂ is the total flow through the contracted section; however, for case 1c, contraction scour should be calculated separately: (a) for the main channel flow, (b) for the flow of the left floodplain, and (c) for the flow of the right floodplain.
In some cases, the values of W₁ and W₂ are not easily definable; therefore, they can be replaced by the values of the width of the flow surface, as long as both widths are used either as bottom or surface. However, width W₂ is normally taken as the bottom width, excluding the width of the pier(s).
In sandy beds, where the hole or depression produced by the contraction is normally filled during the recession of the avenue, the value of y_o can be approximated by that of y₁.
Very coarse sediments can lead to armoring of the bed. In this case, it is recommended to calculate contraction scour by the two methods: (a) live bed, and (b) clear water (see Section 6.3.3). The smallest calculated value should be used for the design.

3.3 Contraction under clear water

Contraction scour under clear-water conditions is calculated using the Laursen formula (1963):

y_s K_u Q²
^_____ = (^{______________}) ^0.43 - 1
y_o D_m^0.67 W²
(3)

in which:

y_s = average depth of contraction scour under clear water, in m or ft;

y_o = average depth of flow under the bridge, before scour, in m or ft;

W = bottom width in the contracted section, excluding the width of the piers, in m or ft;

Q = flow in the contracted section, in m³/sec o ft³/sec;

D_m = diameter of the smallest sediment size in the contracted section, which is not transported, which is assumed equal to 1.25 D₅₀, in m or ft; and

K_u = empirical constant, equal to 0.025 in SI units (metric) and 0.0077 in U.S. customary units.

The minimum value of D₅₀ to use should be 0.0002 m (0.2 mm). Note that the use of a D₅₀ value < 0.2 mm will result in an overestimation of the contraction scour under clear water.

4. LOCAL SCOUR

Local scour is one of the most common causes of bridge failure due to hydraulic stress. The following factors must be taken into account in the calculation of local scour in a pier or abutment:

Flow rate,
Flow depth,
Pier width,
Discharge intercepted by the abutment(s) and eventually returned to the main channel,
Angle of attack of the upstream flow,
Pier length, if the pier is oriented at an angle to the predominant direction of the flow,
Size and granulometric distribution of the bed material,
The condition (configuration) of the bed, that is, the prevailing bedforms, usually during flood,
Shape of the cross section of the pier or abutment,
Formation and/or transport of ice, and
Presence of tree trunks and other vegetative debris transported by the flow.

The depth of scour increases directly with the depth and velocity of flow. Therefore, the risk of failure, usually due to an insufficient foundation depth, increases considerably during the passage of an infrequent or extraordinary flood.

The depth of scour does not directly depend on the size of the bed material. However, in the case of fine materials (silt and clays), the scour velocity is usually smaller compared to that corresponding to coarse materials (sands).

Established formulas for calculating local scour are the following: (1) HEC-18, (2) Jain and Fisher, (3) Froelich, and (4) Melville. These formulas are detailed below.

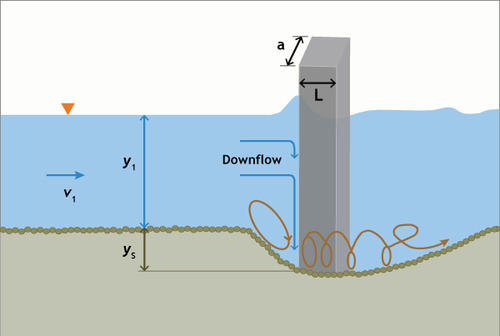
4.1 HEC-18 formula

The HEC-18 formula calculates the maximum depth of scour in sandy fluvial beds. The formula is named after Hydraulic Engineering Circular No. 18 of the Federal Highway Administration (FHWA), of the US Department of Transportation. The HEC-18 formula is the following (Fig. 13):

y_s a
^_____ = 2 K₁ K₂ K₃ (^____) ^0.65 F ^0.43
y₁ y₁
(4)

Fig. 13 Definition sketch for local scour of pier.

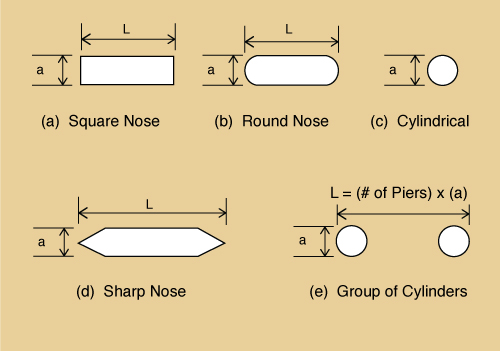
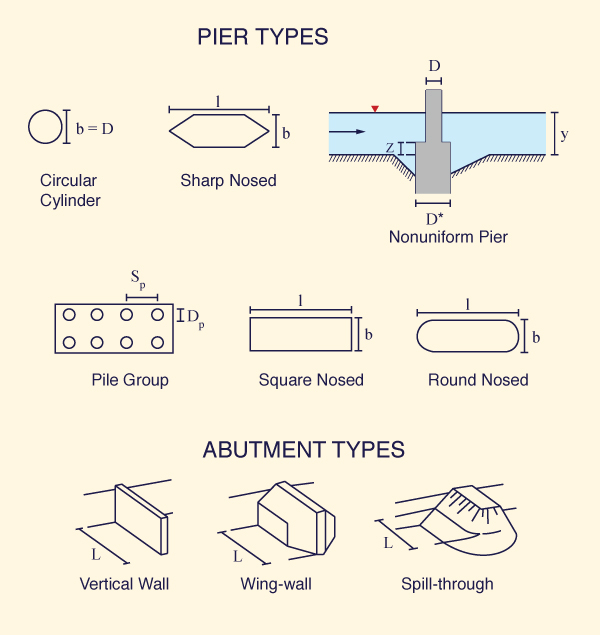
in which

y_s = depth of scour hole, in m;

y₁ = depth of flow immediately upstream of the pier, in m;

v₁ = mean flow velocity immediately upstream of the pier, in m/s;

a = pier width, in m;

F = Froude number = v₁/(gy₁)^1/2;

K₁ = correction factor to take into account the shape of the cross section (Fig. 14 and Table 2);

K₂ = correction factor to take into account the effect of the angle θ between the alignment of the pier and the alignment of the flow (the angle of attack of the flow) (Eq. 5 or Table 3):

L
K₂ = ( cos θ + ^____ sin θ ) ^0.65
a
(5)

in which L = pier length, in m; and θ = pier attack angle;

K₃ = correction factor to take into account the condition of the fluvial bed (Table 26).

Fig. 14 Typical forms of the cross section of a bridge pier.

Table 2 Correction factor K₁.
	Shape of the cross section (See Fig. 14)	K₁
a	Square nose	1.1
b	Round nose	1.0
c	Cilinder	1.0
d	Sharp nose	0.9
e	Group of cylinders	1.0
*Note:* These values are valid for angles of attack θ ≤ 5°. For θ > 5°, assume K₁ = 1.

Table 3 Correction factor K₂.
Angle of attack θ°	L/a (See L and a in Fig. 14)
Angle of attack θ°	4	8	12
0	1.0	1.0	1.0
15	1.5	2.0	2.5
30	2.0	2.75	3.5
45	2.3	3.3	4.3
90	2.5	3.9	5.0
*Note:* These values are valid when the pier length L is subject to the angle of attack θ. The máximum value of K₂ is 5.

Table 4 Correction factor K₃.
	Bedform condition	Height of dune H (m)	K₃
a	Scour with clear water	-	1.1
b	Plane bed with antidunes	-	1.1
c	Small dunes	0.6 - 3	1.1
d	Medium-sized dunes	3 - 10	1.2
e	Large dunes	> 10	1.3
*Note:* Under usual design flow frequencies (case b), K₃ = 1.1. In the presence of de medium-sized or large dunes (cases d or e), the value of K₃ increases as indicated.

Example 1.

Given: (1) flow depth y₁ = 2 m; (2) flow velocity v₁ = 3 m/s; (3) pier width a = 0.5 m; (4) pier length L = 2 m; (5) angle of attack θ of the flow = 0°; (6) square nose pier shape; and (7) plane bed with antidunes. Calculate local scour using formula HEC-18. To check your results, use ONLINE SCOUR HEC-18.

calculator image
CALCULATION ONLINE. Using Eqs. 4 and 5, the depth of local scour is: y_s = 1.66 m. Using ONLINE SCOUR HEC-18: y_s = 1.66 m.

4.2 Jain and Fisher formula

The Jain and Fisher formula is applicable to the calculation of local scour. The formula distinguishes between two types of scour:

Scouring under clear water conditions, for low Froude numbers, and,
Scouring under live bed conditions, for high Froude numbers.

The formulas are the following:

a. Scour under clear water, for the case (F - F_c ) ≤ 0.2:

y_s y
^_____ = 1.84 F_c^0.25 (^____) ^0.3
a a
(6)

b. Scour under live bed, for the case (F - F_c ) > 0.2:

y_s y
^_____ = 2 (F - F_c ) ^0.25 (^____) ^0.5
a a
(7)

in which:

y_s = depth of scour;

a = pier width;

v = mean velocity of the flow immediately upstream;

y = depth of flow immediately upstream;

V_c = critical velocity, at which bed sediment movement starts;

F = Froude number = v/(gy)^0.5; and

F_c = critical Froude number = V_c /(gy)^0.5.

The critical velocity may be estimated using the following.

V_c = K_u y^1/6 D₅₀^1/3

(1)

in which:

V_c = critical velocity necessary for the start of bed sediment movement, in m/sec or ft/sec;

y = depth of flow immediately upstream of the bridge, in m or ft;

D₅₀ = mean diameter of the bed sediment particles located immediately upstream of the bridge, in m or ft;

K_u = empirical constant, equal to 6.19 in the SI system (metric), and 11.17 in the U.S. customary system of units;

To obtain the D₅₀ of the bed material, it must be sampled in the first 0.3 m depth. Eq. 206a is applicable to granular materials, being restricted to values of D₅₀ ≥ 0.0002 m (0.2 mm). For smaller sizes, cohesion has the effect of increasing the critical velocity.

Example 2.

Given: (1) flow depth y = 2 m; (2) flow velocity v = 3 m/s; (3) pier width a = 0.5 m; (4) mean diameter of the bed material D₅₀ = 1 mm. Calculate the local scour using the Jain and Fisher formula. For checking, use ONLINE SCOUR JAIN AND FISHER.

calculator image
ONLINE CALCULATION. Using Eq. 7, the local scour depth is: y_s = 1.698 m. Using ONLINE SCOUR JAIN AND FISHER: y_s = 1.698 m.

4.3 Froehlich's formula

Froehlich's formula is frequently used for the calculation of local scour in a bridge pier (Fig. 15). The version of the formula applicable for design is:

y_s b_e y_o b
^_____ = 0.32 φ (F_r₁ )^0.2 (^____) ^0.62 ( ^____ )^0.46 ( ^_____ )^0.08 + 1
b b b D_₅₀
(8)

in which:

y_s = scour depth (L units);

b = pier width (L units);

D_₅₀ = mean particle diameter (L units);

b_e = projection of the pier width b in a plane normal to the angle of attack θ (L units);

φ = dimensionless coefficient which accounts for the form of the cross section (see Fig. 14): φ = 1.3 for square nose; φ = 1.0 for round nose; and φ = 0.7 for sharp nose;

v₁ = mean velocity immediately upstream of the pier (L /T units);

y₁ = flow depth immediately upstream of the pier (L units);

F_r₁ = Froude number immediately upstream of the pier: F_r₁ = v₁ /(gy₁)^0.5;

Equation 8 is dimensionless when used with consistent units (m or ft).

Fig. 15 Detail of Petty Creek Road bridge pier, on the Clark river, near Alberton, Montana.

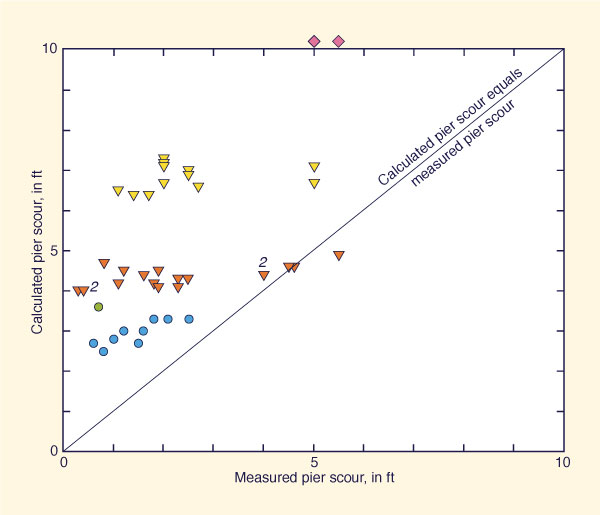
Figure 16 shows an evaluation of Eq. 8, Note that the calculated values are almost always greater than the measured values. Also, note that Froehlich's formula is one of those included in HEC-RAS.

Fig. 16 Evaluation of Froehlich's design formula.

Example 3.

Given: (1) flow depth y = 2 m; (2) flow velocity v = 3 m/s; (3) pier width b = 0.5 m; (4) angle of attack of the flow θ = 0°; (5) mean diameter of bed material D₅₀ = 1 mm; and (6) square nose pier. Calculate the l.ocal scour applicable for design using Froehlich's 1988 formula. To check, use ONLINE SCOUR FROEHLICH 1988.

ONLINE CALCULATION. Using Eq. 8, the local scour depth is: y_s = 1.098 m. Using ONLINE SCOUR FROEHLICH 1988: y_s = 1.098 m.

4.4 Melville's formula

Melville's formula calculates the maximum depth of local scour on a bridge pier or abutment. The formula is based on a product of six empirical variables K, each of which evaluates a contributing factor to local scour. The formula is:

d_s = K_yW K_i K_d K_s K_θ K_G

(9)

in which:

d_s = maximum depth of local scour, in units of length (m or ft);

K_yW = depth factor: (a) K_yb for piers, o (b) K_yL for abutments, in units of length (m or ft);

K_I = factor of flow intensity, including effects of sediment gradation and flow velocity, dimensionless;

K_d = factor of sediment size; dimensionless;

K_s = factor of shape of the pier or abutment; dimensionless;

K_θ = factor of alignment of the pier or abutment; dimensionless; and

K_G = factor of geometry of the canal; dimensionless.

Equation 9 evaluates the local scour of piers or abutments in cases where contraction scour is negligible.

Depth factor for piers or abutments

The depth factor K_yW (K_yb for piers or K_yL abutments) is given by one of the following equations:

K_yb = 2.4 b [for narrow piers ⇒ (b /y ) ≤ 0.7]

(10a)

K_yb = 2 (yb )^0.5 [for intermediate piers ⇒ 0.7 < (b /y ) ≤ 5.0]

(10b)

K_yb = 4.5 y [for wide piers ⇒ (b /y ) > 5.0]

(10c)

K_yL = 2 L [for short abutments ⇒ (L /y ) ≤ 1]

(11a)

K_yL = 2 (yL )^0.5 [for intermediate abutments ⇒ 1 < (L /y ) ≤ 25]

(11b)

K_yL = 10 y [for long abutments ⇒ (L /y ) > 25]

(11c)

in which:

y = flow depth immediately upstream of the pier or abutment;

b = pier width; y

L = abutment length, including the bridge approximation, projected in a direction perpendicular to the flow.

Flow intensity factor

Regarding the flow intensity factor, it is necessary to distinguish between two types of local scour: (1) under clear water, and (2) under live bed, as in the case of the Jain and Fisher formula (Section 4.2). Scouring under clear water occurs before the start of the movement of the bed, and scour under live bed after the start of movement.

Scouring under clear water typically occurs in the floodplain. Scouring under live bed occurs when there is sediment transport in the vicinity of the hole. If the sediment is uniform, that is, with a gradation coefficient σ_g ≤ 1.3, armoring is not produced. Conversely, if the sediment is nonuniform, with a gradation coefficient σ_g > 1.3, armoring is effectively produced, which reduces the depth of the scour hole. [The gradation coefficient is: σ_g = (d₈₄/d₁₆)^1/2].

The flow intensity factor K_I is given by one of the following equations:

K_I = [V - (V_a - V_c )] / V_c {for [V - (V_a - V_c )] / V_c < 1}

(12a)

K_I = 1 {for [V - (V_a - V_c )] / V_c ≥ 1}

(12b)

in which:

V = mean flow velocity immediately upstream;

V_c = mean flow velocity immediately upstream, at the onset of bed movement;

V_a = mean flow velocity immediately upstream, at the start of live bed movement (for uniform sediments, V_a = V_c; for nonuniform sediments, V_a > V_c);

V_a = 0.8 V_ca; and

V_ca = mean flow velocity beyond which armoring of a nonuniform sediment bed is impossible

The velocities V_c and V_ca are calculated with the following formulas:

V_c y
^_____ = 5.75 log ( 5.53 ^_____ )
u_{_{_*c}} d_₅₀
(13)

V_ca y
^______ = 5.75 log ( 5.53 ^______ )
u_{_{_*ca}} d_{_50a}
(14)

in which:

d_₅₀ = mean particle diameter (mm);

d_{_50a} = d_{_max} / 1.8; and

d_{_max} = máximum particle diameter (mm).

For quartz sediments at the temperature of T = 20°C, the shear velocities u_{_{_*c}} y u_{_{_*ca}} are estimated as follows:

u_{_{_*c}} = 0.0115 + 0.0125 d_₅₀^1.4 [for 0.1 mm ≤ d_₅₀ < 1 mm]

(15a)

u_{_{_*c}} = 0.0305 d_₅₀^0.5 - 0.0065 d_₅₀^-1 [for 1 mm ≤ d_₅₀ < 100 mm]

(15b)

u_{_{_*ca}} = 0.0115 + 0.0125 d_{_50a}^1.4 [for 0.1 mm ≤ d_{_50a} < 1 mm]

(16a)

u_{_{_*ca}} = 0.0305 d_{_50a}^0.5 - 0.0065 d_{_50a}^-1 [for 1 mm ≤ d_{_50a} < 100 mm]

(16b)

Factor of sediment size

The factor of sediment size K_d is given by one of the following equations:

                                     W
K_d = 0.57 log ( 2.24 ^_____ )                     [for W /d_₅₀ ≤ 25]
                                    d_₅₀

(17a)

K_d = 1 [for W /d_₅₀ > 25]

(17b)

in which W = b for piers, and W = L for abutments.

Factor of shape of the pier or abutment

The shape factor K_s is shown in Table 5, with reference to Fig. 17.

*Table 5 Shape factor K_s* .**
		Cross section (see Fig. 101)	K_s
Pier	a	Circular cylinder	1.0
	b	Round nose	1.0
	c	Square nose	1.1
	d	Sharp nose	0.9
Abutment	a	Vertical wall	1.0
	b	Wing wall	0.75
	c	Spill at 0.5 H : 1 V	0.6
	d	Spill at 1 H : 1 V	0.5
	e	Spill at 1.5 H : 1 V	0.45

Fig. 17 Tipos de pilares y estribos (Melville, 1997).

For long abutments, the shape factor is not too important. Therefore, the factor K_s shown in Table 4 should be replaced by the following modified factor K*_s:

K*_s = K_s [for short abutments ⇒ (L / y ) ≤ 10 ]

(18a)

K*_s = K_s + 0.667 (1 - K_s ) [ 0.1 (L/y ) - 1 ] [for intermediate 10 < (L / y ) < 25 ]

(18b)

K*_s = 1 [for long abutments ⇒ (L / y ) ≥ 25 ]

(18c)

Factor of alignment of the pier or abutment

The alignment factor K_θ is shown in Table 6. Note that for the case of piers, these values are the same as the correction factors K₁ shown in Table 2.

Table 6 Alignment factor K_θ .
Attack angle θ°	K_θ for piers			K_θ for abutments
	L/a (see L and a in Fig. 14)
	4	8	12
0	1.0	1.0	1.0	-
15	1.5	2.0	2.5	-
30	2.0	2.75	3.5	0.9
45	2.3	3.3	4.3	-
60	-	-	-	0.97
90	2.5	3.9	5.0	1.0
120	-	-	-	1.06
150	-	-	-	1.08

The factor K_θ for abutments applies only for the case of long abutments. Therefore, this value is to be replaced by the following modified factor K*_θ :

K*_θ = 1 [for short abutments ⇒ (L / y ) ≤ 1 ]

(19a)

K*_θ = K_θ + (1 - K_θ ) [ 1.5 - 0.5 (L / y ) ] [for intermediate 1 < (L / y ) < 3 ]

(19b)

K*_θ = K_θ [for long abutments ⇒ (L / y ) ≥ 3 ]

(19c)

Factor of geometry of the canal

In the case of a pier, the geometry of the canal does not affect the amount of scour. Therefore, the factor of geometry for a pier is K_{_G} = 1.

In the case of an abutment, the factor of geometry K_{_G} is given by the following formula:

Left abutment

                       L*_{_i}                 y*_{_i}             n
K_{_G} = { 1 - ^______ [ 1 - ( ^____ ) ^5/3 ^____ ] }^1/2
                       L_{_i}                   y              n*_{_i}

(20a)

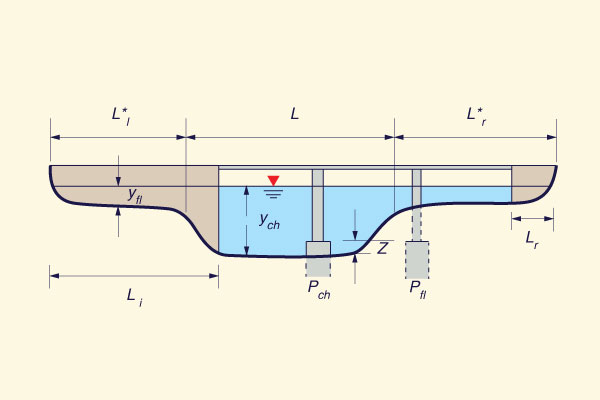
in which (Fig. 18):

L_{_i} = length of left abutment;

L*_{_i} = width of the flood plain on the left abutment;

y = flow depth in the main channel;

y*_{_i} = flow depth in the flood plain on the left abutment;

n = Manning coefficient in the main channel; and

n*_{_i} = Manning coefficient in the flood plain of the left abutment.

Right abutment

                       L*_{_r}                 y*_{_r}             n
K_{_G} = { 1 - ^______ [ 1 - ( ^____ ) ^5/3 ^____ ] }^1/2
                       L_{_r}                   y              n*_{_r}

(20b)

in which (Fig. 18):

L_{_i} = length of right abutment;

L*_{_i} = width of the flood plain on the right abutment;

y = flow depth in the main channel;

y*_{_i} = flow depth in the flood plain on the right abutment;

n = Manning coefficient in the main channel; and

n*_{_i} = Manning coefficient in the flood plain of the right abutment.

Fig. 18 Definition sketch for Eq. 219.

5. UNCONVENTIONAL STREAM CROSSINGS

In nature, rivers are classified into: (1) perennial, (2) intermittent, and (3) ephemeral. Perennial rivers always have water, which originates in the baseflow [Fig. 19 (a)]. Intermittent rivers have water only a few months a year, with low water flows sustained by seasonal groundwater flows [Figs. 19 (b) and (c)]. Ephemeral rivers have water only during and immediately following a precipitation event [Fig. 19 (d)]. The position of the water table, above, at the level, or below the streambed, determines if it is perennial, intermittent, or ephemeral, respectively.

Fig. 19 (a) Indian Creek, California.

Fig. 19 (b) Gila river, Arizona.

Fig. 19 (c) Rosarito Creek, Baja California, Mexico.

Fig. 19 (d) Mojave river, California.

The depth to the water table varies across the climatic spectrum, from arid regions to humid regions. In humid areas, the water table is close to the surface, while in arid areas it is found at much greater depths. In general, the drier the climate, the greater the depth to the water table. Therefore, ephemeral rivers are quite common in arid regions. The peak of erosion and sediment transport occurs around an average annual precipitation of 375 mm (15 inches), which corresponds to an arid region (200-400 mm) (Ponce et al., 2000). Therefore, rivers located in arid regions usually transport large amounts of sediment.

From a geomorphological perspective, when a river carries a large amount of sediments, the width-depth ratio is large, typically between 50 and 100. Therefore, river crossings in arid regions represent a considerable challenge for design. The problem is how to make possible the crossing of an ephemeral river in an effective and economic way.

River bridges can be of various types; in principle they must cover the entire width of the river (Fig. 20). When the bridges do not cover the entire width of the river, this leads to problems during the floods. Generally, during a flood the river reclaims its actual width, endangering the foundation and, consequently, the stability of the structure. Excessive speeds in the vicinity of piers or abutments can cause local erosion and lead to the eventual failure of the bridge.

Fig. 20 Bridge over the Santa Catarina river, in Monterrey, Nuevo León, México.
This unusual bridge, supported on only one side, in operation since 2003,
withstood the passage of Hurricane Alex on July 1, 2010.

The bridges are built when the volume of traffic and/or the importance of the road network justify the cost. Most bridges are permanent structures, vulnerable to extreme floods. Rivers, particularly those located in arid regions, can overflow their channels, or even change course, making the crossing structure inoperable (Fig. 8).

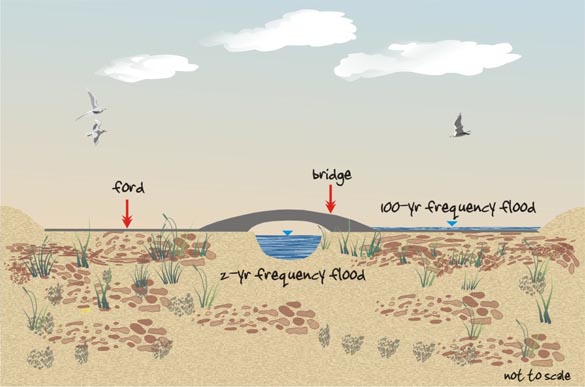
5.1 The ford crossing

A ford is a temporary or permanent structure to cross a river or stream, without the full benefit of a bridge. The ford is a design alternative in cases of light traffic or limited resources. The constructed fords are designed to cross the river on a concrete slab for cases where the flow is small or non-existent (Fig. 21). In arid regions, fords are common in places where water flows only a few days out of the year (Fig. 22). The ford is an economical way to solve the problem of crossing a river.

gran vado sobre el rio jaguaribe, ceara, brasil

Fig. 21 A large ford in Jaguaribira, on the Jaguaribe river, Ceara, Brasil.

Fig. 26 A large ford on Guadalupe Creek, Baja California, Mexico.

The disadvantage of a ford is that it may be out of service a few days out of the year, but when this is compared to the cost of a bridge, the decision may be justified. Fords are generally used in rural areas, where traffic and/or economic resources are limited.

A singular case of the crossing of an important river by means of a built ford is that of El Cora ford, which is designed to operate on the El Jileño diversion dam, on the Rio Grande de Santiago, near Tepic, Nayarit, Mexico. The length of the dam and ford is 473 m (Figs. 27 and 28). The video Vado El Cora describes this unusual structure.

Google Earth^®

Fig. 27 Aerial view of El Jileño diversion dam, on the Río Grande de Santiago, Nayarit, México.

Fig. 28 Crossing of El Cora ford on top of El Jileño diversion dam.

During extraordinary floods, fords are also subject, like bridges, to hydraulic erosion, possible failure and consequent inoperability. Figure 29 shows a ford on Indian Trail Road, on the Mojave River, near Helendale, California: (a) during the failure, in March 2005, and (b) some time after the failure.

Linda Hoover

Fig. 29 (a) Ford on Indian Trail Road, on the río Mojave, during the flood of 2005.

Fig. 29 (b) Intersection of Indian Trail Road with the Mojave river in June of 2005,
sometime after the failure of the ford.

5.2 The Arizona crossing

The Arizona crossing is a type of ford used in the southwest of the United States for the crossing of ephemeral river channels. The ford consists of a predetermined group of circular culverts, usually of corrugated aluminum, aligned to form an embankment, enabling the passage of vehicles on top of it (Fig. 30). The length of the embankment usually comprises the main channel of the stream or river. This type of crossing is designed for a limited overflow in the case of an infrequent or extraordinary flood. There is the possibility of partial or total failure of the embankment as a result of excessive erosion during a major flood.

Boys Scouts' Irvine Ranch

Fig. 30 The Arizona crossing, Orange county, California.

The culvert bridge (Fig. 31) is similar to the Arizona crossing. The difference is that the culvert bridge is not designed for an eventual spillover. During an extraordinary flood, the overflow may endanger the integrity of the structure.

Fig. 31 Culvert bridge, Tecate Creek, Baja California, Mexico.

5.3 The ford-bridge

A ford-bridge is a combination of ford and bridge, with a maximum of advantages and a minimum of disadvantages. The ford-bridge is designed to work as a bridge during periods of low flow and as a ford during high flows. In an ephemeral river, a ford-bridge resembles a ford for the most part, but contains a relatively small bridge, designed to pass the mean annual flood (Fig. 32).

Fig. 32 Artist's rendition of a ford-bridge.

The ford-bridge can span at comparatively small cost the total width of the river. There is no need to shorten the width of the structure and there are no bridge piers that can fail during an extraordinary flood. Essentially, the ford-bridge works as a ford during extraordinary floods; at all other times, the ford-bridge serves as a bridge. For ephemeral rivers in arid regions, the ford-bridge provides a suitable combination of functionality and economy.

All river crossings are designed to sustain a specific hydrologic load. This is usually the 100-yr flood, and in some cases, even greater. In a typical bridge design, peak flow is expressed in terms of depths and velocities and these data are used to calculate local scour on piers and abutments. In contrast, a ford has no piers; the only design requirement is the proper anchoring of the slab to minimize the possibility of lifting [Note the lack of an anchored slab in Fig. 29 (a)]. As in the case of a bridge, the possibility of failure always exists during extreme floods.

The components of a ford-bridge must be designed as fords and bridges, respectively. The design of the ford component is of the conventional type; however, the bridge component is much smaller than a typical bridge. The design of the bridge may be based on the average annual flood, that is, the 2-yr flood, which, from a geomorphological perspective, is formative of the main channel. This contrasts with the 100-yr flood used in the design of conventional bridges. During extreme events, the ford distributes the hydraulic load across the entire channel width. Therefore, the ford-bridge is in an optimal position to withstand the loads and stresses typical of extraordinary floods.

The ford-bridge is a practical alternative to the conventional bridge or ford. The concept is applicable in ephemeral rivers featuring a large width-to-depth ratio, particularly in rural areas, or where traffic is light and resources are limited. The design of the ford-bridge optimizes the hydrologic loads, using the bridge for the 2-yr flood and the ford for the 100-yr flood. The ford-bridge is an appropriate solution for wide river crossings for predominantly rural areas in arid regions.

Figure 33 shows a bridge over the Fuerte river, in Guasave, Sinaloa, Mexico, designed to withstand an overflow by relatively frequent floods; therefore it qualifies as a ford-bridge.

Fig. 33 Pepe Chuy Sanchez puente vado (ford bridge) on the Fuerte river, Guasave, Sinaloa, Mexico.

6. LONGEVITY OF A BRIDGE

Based on what is presented in Sections 6.3 to 6.5, it can be concluded that the longevity of a bridge depends on whether its as-built length respects the hydraulic integrity of the river it crosses. For example, the Roman bridge over the Guadiana river, in Merida, Spain, dating back to the 1st century B.C., is still in operation (although only in the pedestrian mode), having been partially restored several times (Fig. 34). With a height of 12 m and a length of 792 m in 60 arches, the bridge occupies a large part of the floodplain of the large and regionally important Guadiana river.

Fig. 34 (a) Roman bridge spanning the Guadiana river, near Merida, Extremadura, Spain.

Wikimedia Commons

Fig. 34 (b) Closeup of the roman bridge on the Guadiana river.

Another example of bridge longevity is the ancient Inca bridge, located near the headwaters of the Lauricocha River, in Huanuco, Peru, for which an age of more than 500 years has been reported. Figure 35 clearly shows that this bridge, 60 m long and with a total of 24 bays, is approximately six (6) times longer than the dry-season width of the river.

Eduardo Figari

Fig. 35 Ancient Inca bridge, near the headwaters of the Lauricocha river, Huanuco, Peru.

http://ponce.sdsu.edu/bridge_scour_1.html 201124 17:00

ruler