COMPARISON BETWEEN CLARK'S ORIGINAL AND CLARK'S PONCE UNIT HYDROGRAPHS Andrea C. Scott and Victor M. Ponce [201220] Abstract. The theoretical basis for Clark's original 1945 and Clark's Ponce 1989 methods of catchment routing are explained and compared. It is shown that Ponce's method consistently provides a somewhat longer time base and a correspondingly smaller peak discharge than Clark's original methodology. This is a direct consequence of Ponce's use of a continuous time-area derived unit hydrograph, in lieu of the discrete hyetograph used by Clark. However, the differences in peak discharge are consistent with the methodologies used and do not appear to be significant. 1.  INTRODUCTION Catchment routing is the field of runoff analysis that converts effective rainfall into runoff. It considers both spatial and temporal variations in transforming effective rainfall into a flowrate. The solution approach may be either a simple lumped model or a more sophisticated distributed model. The former is a spatially lumped model that calculates runoff as a function of time only, while the latter is a function of space and time throughout the catchment (Fig. 1). NOAA/ NWS/The COMET Program Fig. 1  Lumped vs distributed catchment models. In catchment routing, the components of translation and storage constitute two distinct processes used to transform an inflow hyetograph into an outflow hydrograph. Translation is interpreted as the movement of water parallel to the channel bottom; storage is interpreted as the movement of water perpendicular to the channel bottom. Translation is often referred to as convection or concentration; storage is referred to as diffusion or attenuation. The Clark model is an established method for calculating a unit hydrograph (Clark, 1945). The procedure consists of a two-step process: (1) first, the use of the time-area method for the translation component; and (2) second, the use of a linear reservoir for the diffusion component (Ponce, 1989a). Clark obtained a hyetograph of unit runoff from the first step and proceeded to route this hyetograph through a linear reservoir for the second step. Ponce modified the Clark procedure by obtaining a hydrograph of unit runoff out of the first step, and subsequently routing this hydrograph through a linear reservoir (Ponce, 1989a). Ponce's procedure provides a slightly more diffused unit hydrograph, albeit one that is more consistent with established routing principles. Both procedures, Clark's original and Clark's Ponce are documented and compared in this paper. 2.  METHODOLOGY The methodology for developing the first part of a Clark unit hydrograph resembles that of the time-area method. First, the catchment is divided into several subcatchments delimited by isochrones, defined as lines of equal travel time to the outlet [Fig. 2 (a)]. The resulting subareas are measured and plotted for each time interval, constituting a time-area histogram [Fig. 2 (b)]. To develop the flows, the histogram subareas are multiplied by the unit effective rainfall intensity to produce a discrete unit-runoff hyetograph. Fig. 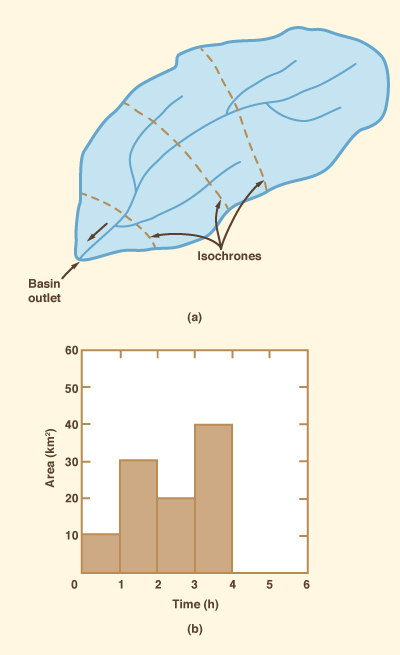2  Time-area method: (a) isochrones; and (b) time-area histogram. The procedure leads to a hyetograph corresponding to a unit depth of effective runoff. Since this hyetograph has no provision for runoff diffusion, Clark provided the missing diffusion in a second step, by routing the unit-runoff hyetograph through a linear reservoir. Despite the lack of diffusion, a hyetograph/hydrograph developed using the time-area method has the inherent advantage of taking into account the catchment shape. Fan-shaped catchments lead to narrow-peaked hydrographs, whereas elongated catchments produce broader hydrographs (Fig. 3). Fig. 3  Effect of catchment shape on a hydrograph (Subramanya, 1994). 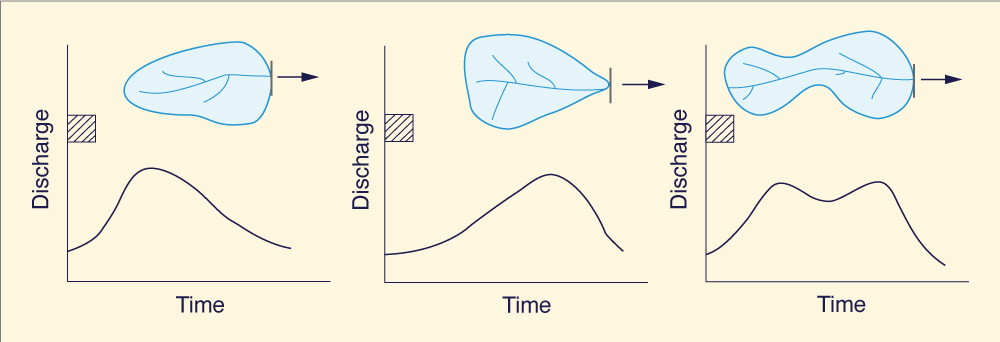The second part of the Clark method is designed to provide runoff diffusion. The amount of diffusion depends on the routing coefficient K of the linear reservoir, particularly on the ratio Δt/K, where Δt is the chosen time interval, or time step. In computational hydraulics, this ratio is referred to as the Courant number. The effect of the Courant number can be readily ascertained by an examination of the SSARR routing equation (Eq. 1), which is based on linear reservoir theory (Ponce, 1989b). For a value C = 2, the multiplier outside of the brackets goes to 1, and the resultant outflow is equal to the average inflow, effectively simulating a rational method hydrograph, which ostensibly features zero diffusion. Values of C < 2 provide varying amounts of diffusion, whereas values of C > 2 provide negative diffusion, i.e., an amplification effect and are therefore, not applicable in catchment routing.                        2 C Q j+1n+1 =   _________ [ Q̄ j  -  Q j+1n ]  +  Q j+1n                      2 + C (1) Figure 4 illustrates a sequence of hydrographs for Courant numbers varying between 0.1 and 2 (Ponce, 1980). This figure shows that the diffusion effect increases with a decrease in Courant number. Fig. 4  Computed hydrographs as a function of Courant number. Clark's Ponce unit hydrograph methodology preserves the philosophy and intent of the original Clark method while introducing a slight modification, or improvement. Rather than routing a discrete unit-runoff hyetograph through a linear reservoir as in Clark's original method, Ponce routes a continuous unit-runoff hydrograph. This results in a slight increase in time base and a concomitant reduction in peak flow, as shown by Ponce and Nuccitelli (2013). 3.  ANALYSIS The Clark original unit hydrograph and Clark Ponce's unit hydrograph were compared by varying: (1) isochrone definition, (2) Courant number, and (3) drainage area. Ponce's online calculators ONLINE ROUTING CLARK and ONLINE ROUTING CLARK 2 were used in the analysis. In particular, the second calculator was used for the cases which required a longer time base. Initially, a 100-km2 catchment was assumed, with five (5) isochrone definition scenarios to simulate an array of catchment shapes (Table 1 and Fig. 5). The purpose was twofold: (1) to show that postulated catchment shapes are readily reflected in the runoff hydrograph; and (2) to confirm that Clark's Ponce methodology consistently provides a somewhat slower response and slightly smaller peak than Clark's original method. Table 1.  Hypothetical drainage area distributions. Scenario Catchment area (km2) Ordered subareas (km2) 1 100 10, 20, 30, 40 2 100 5, 10, 25, 60 3 100 25, 25, 25, 25 4 100 40, 30, 20, 10 5 100 60, 25, 10, 5 Fig. 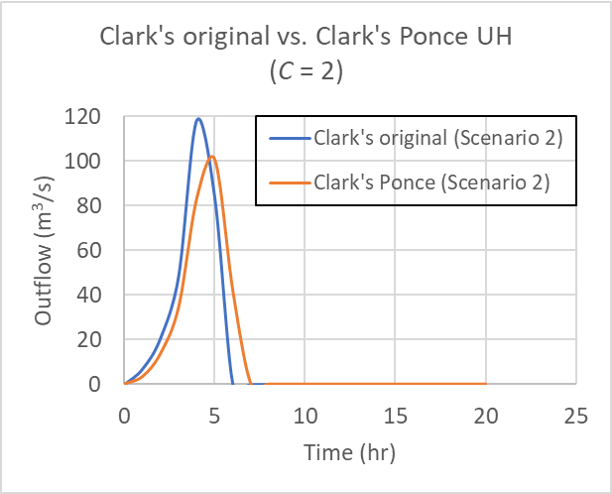5 (a)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 1 (10, 20, 30, 40), for Courant number C = 2. Fig. 5 (b)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 2 (5, 10, 25, 60), for Courant number C = 2. Fig. 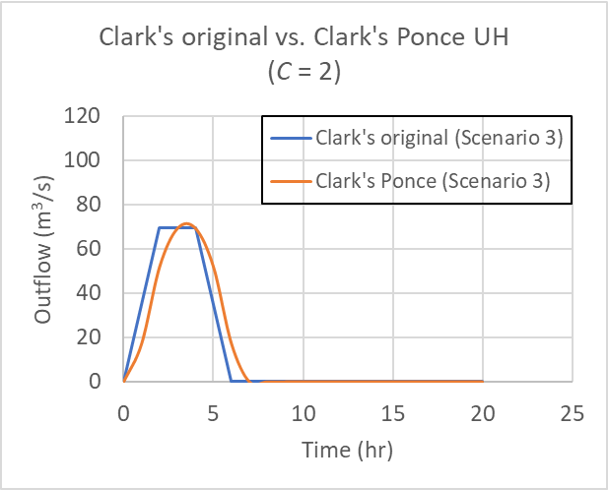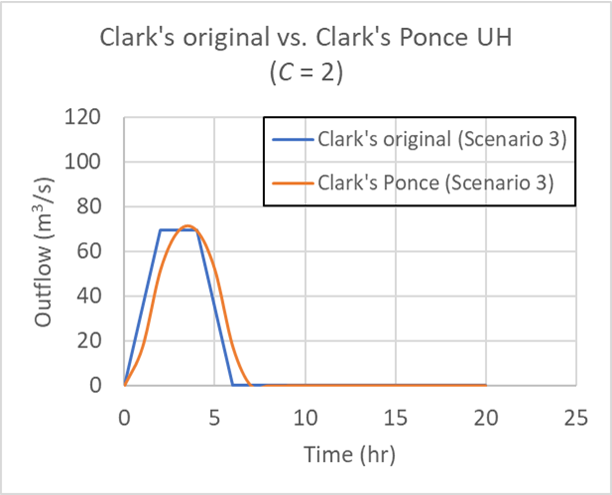5 (c)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 3 (25, 25, 25, 25), for Courant number C = 2. Fig. 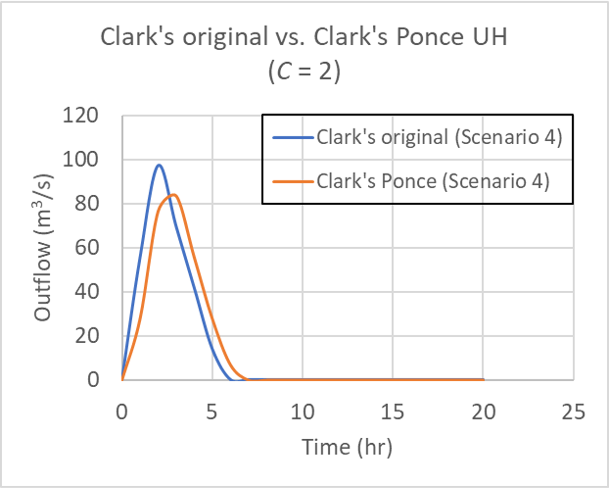5 (d)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 4 (40, 30, 20, 10), for Courant number C = 2. Fig. 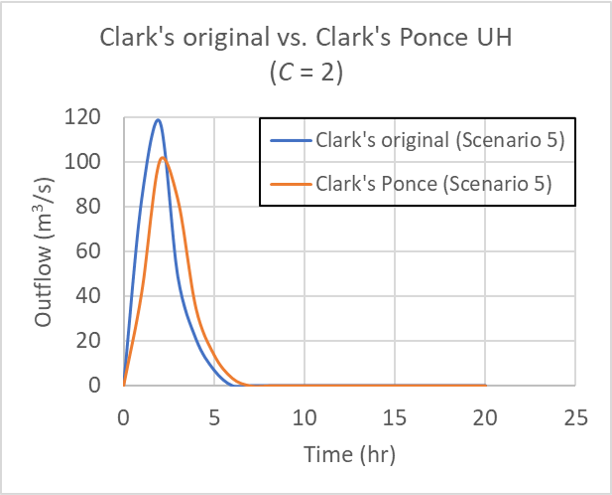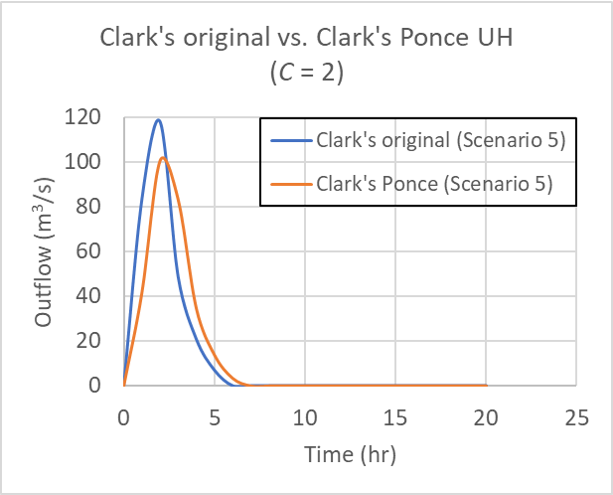5 (e)  Comparison between Clark's original and Clark's Ponce unit hydrographs for for Table 1 Scenario 5 (60, 25, 10, 5), for Courant number C = 2. Courant values ranging from 0.1 to 2 were specified to obtain various amounts of diffusion, as shown in Fig. 6. These results confirm that Clark's Ponce unit hydrograph produces a slightly longer time base and a smaller peak discharge than Clark's original methodology. Figure 6 illustrates the results for Scenario 1 of Table 1. Similar results were observed for Scenarios 2 to 5. Fig. 6 (a)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 1, for Courant number C = 2. Fig. 6 (b)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 1, for Courant number C = 0.8. Fig. 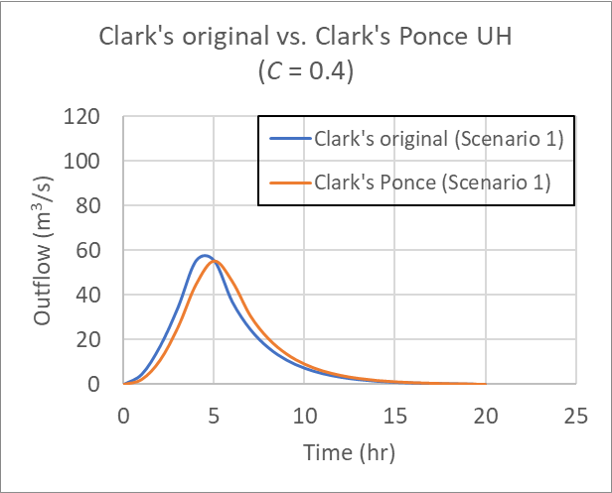6 (c)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 1, for Courant number C = 0.4. Fig. 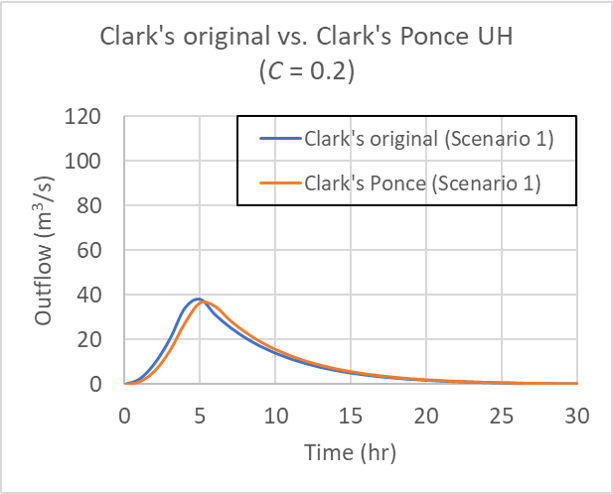6 (d)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 1, for Courant number C = 0.2. Fig. 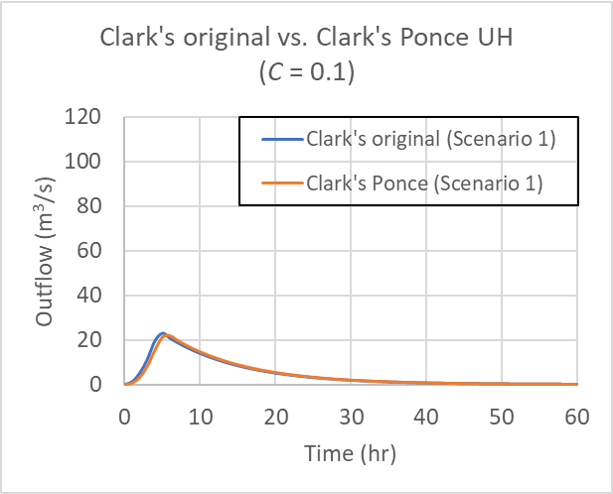6 (e)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 1 Scenario 1, for Courant number C = 0.1. 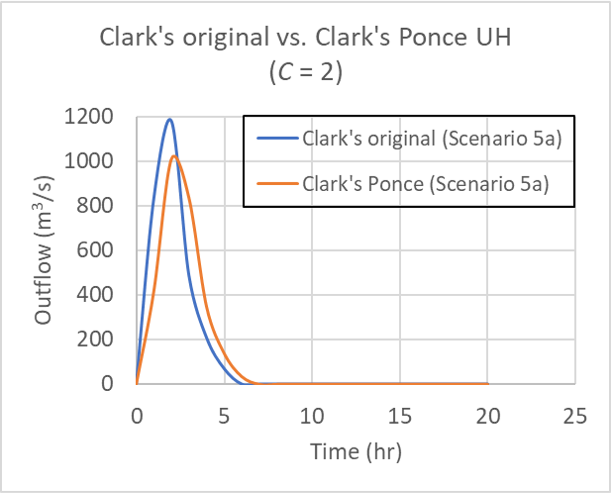To test the effect of catchment area, a catchment area of 1,000 km2 was specified, that is, 10 times the magnitude of the previous value (100 km2), as shown in Table 2. Figure 7 shows that there is no observable differences in the hydrograph shapes. Table 2.  Hypothetical drainage area distributions for two selected catchment areas. Scenario Catchment area (km2) Ordered subareas (km2) 1 100 10, 20, 30, 40 3 100 25, 25, 25, 25 5 100 60, 25, 10, 5 1a 1000 100, 200, 300, 400 3a 1000 250, 250, 250, 250 5a 1000 600, 250, 100, 50 Fig. 7 (a)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 2 Scenario 1 (left) and Scenario 1a (right); C = 2. Fig. 7 (b)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 2 Scenario 3 (left) and Scenario 3a (right); C = 2. Fig. 7 (c)  Comparison between Clark's original and Clark's Ponce unit hydrographs for Table 2 Scenario 5 (left) and Scenario 5a (right); C = 2. 4.  SUMMARY The theoretical basis for Clark's original (1945) and Clark's Ponce (1989) methods of catchment routing are explained and compared. The effect on the unit hydrograph of: (1) catchment shape, (2) Courant number, and (3) catchment area, is elucidated. It is shown that Ponce's method consistently provides a somewhat longer time base and a correspondingly smaller peak discharge than Clark's original methodology. This is a direct consequence of Ponce's use of a continuous time-area derived unit hydrograph, in lieu of the discrete hyetograph used by Clark. However, the differences in peak discharge are consistent with the methodologies used and do not appear to be significant. REFERENCES Clark, C. O., 1945. Storage and the unit hydrograph. Transactions, ASCE, Vol. 110, Paper No. 2261, 1419-1446. Ponce, V. M. 1980. Linear reservoirs and numerical diffusion. Journal of the Hydraulics Division, ASCE, 691-699. Ponce, V. M. 1989a. Engineering Hydrology: Principles and Practices, Section 10.2. Englewood Cliffs, New Jersey, Prentice Hall. Ponce, V. M. 1989b. Engineering Hydrology: Principles and Practices, Section 10.3. Englewood Cliffs, New Jersey, Prentice Hall. Ponce, V. M., and N. R. Nuccitelli. 2013. Comparison of two types of Clark unit hydrographs. Online article. Subramanya, K. 1994. Engineering Hydrology. McGraw-Hill, New Delhi.