|
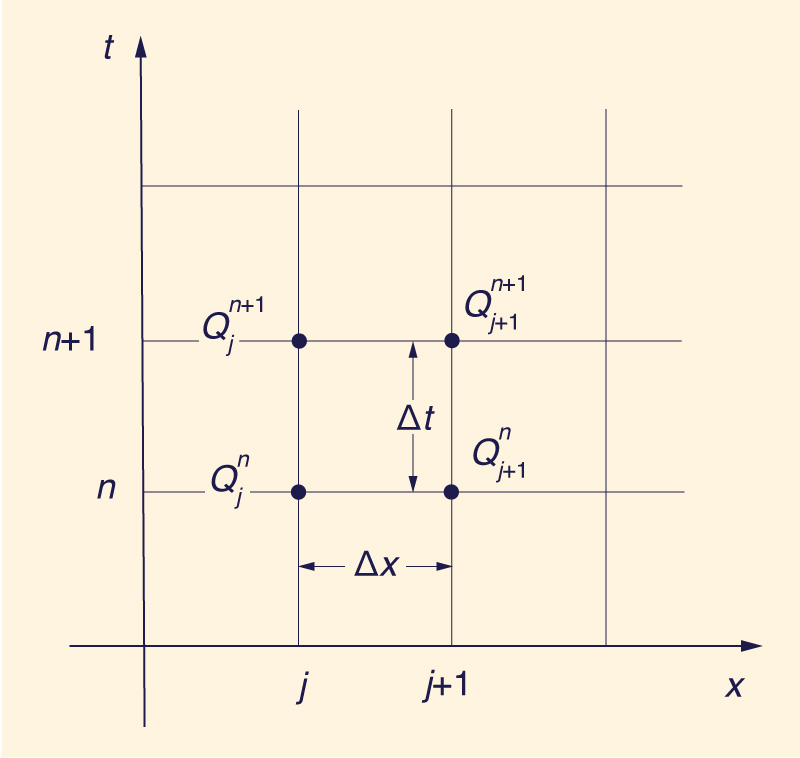
Fig. 1 Discretización espacio-temporal en el método Muskingum.
El tomar la derivada del tiempo en la sección aguas abajo equivale a suponer un almacenamiento de tipo embalse. Por lo tanto, en soluciones discretas, la suposición de un embalse lineal proporciona el mecanismo por el cual se introduce la difusión numérica en los cálculos, para simular los procesos de difusión física en el entorno de la cuenca.
La extensión del efecto de difusión numérica al concepto de cascada de embalses lineales es fácilmente entendible. Al hacerlo, se introduce un segundo parámetro, n, el cual representa el número de embalses en serie. El modelo de dos parámetros {K, n} aumenta la flexibilidad del proceso de simulación, a la vez que se mantiene dentro del marco computacional establecido por el modelo de un parámetro.
2. ENRUTAMIENTO DE ONDAS CINEMÁTICAS Y DIFUSIÓN NUMÉRICA
Cunge (2) fue pionero en establecer el rol de la difusión numérica en relación con el enrutamiento de ondas cinemáticas. Cunge razonó que dado que la ecuación de la onda cinemática es de convección pura, la difusión calculada por un esquema numérico basado en esta ecuación tiene que originarse en el esquema mismo. él rastreó el origen de este efecto de difusión numérica a los errores de truncamiento que surgen de "descentrar" el término de la derivada temporal. Esto propició a una mejor comprensión de las técnicas de enrutamiento de ondas cinemáticas, entre las cuales el método Muskingum es un ejemplo notable. El desarrollo del método Muskingum-Cunge se revisa brevemente en este artículo.
La ecuación de la onda cinemática tiene la siguiente forma:
∂Q ∂Q
_____ + c _____ = 0
∂t ∂x
| (3) |
en la cual Q = caudal; c = celeridad de la onda cinemática; t = variable de tiempo; y x = variable de espacio. La celeridad de la onda cinemática se toma como constante (el caso lineal) o variable con el flujo (el caso cuasilineal) (4,6,8). En el caso lineal, la discretización de la Ec. 3 en el plano x-t (Fig. 1) conduce a la conocida fórmula de Muskingum (1):
|
Q j+1 n+1 = C1Q j n + C2 Q j n+1 + C3 Q j+1 n
| (4) |
en las cuales C1, C2 y C3 son coeficientes definidos como sigue:
Δt
______ + 2X
K
C1 = _______________________
Δt
______ + 2 ( 1 - X )
K
| (5) |
Δt
______ - 2X
K
C2 = _______________________
Δt
______ + 2 ( 1 - X )
K
| (6) |
Δt
2 ( 1 - X ) - ______
K
C3 = _______________________
Δt
______ + 2 ( 1 - X )
K
| (7) |
en las cuales Δx = longitud de tramo; Δt = intervalo de tiempo; K = tiempo de translación (K = Δx /c); y X = factor de ponderación del término de derivada temporal.
Se puede obtener una estimación del valor de X haciendo coincidir el coeficiente de difusividad numérica de la ecuación de la onda cinemática discretizada, con el coeficiente de difusión física de la ecuación de convección-difusión, es decir la ecuación de la onda difusiva. Esto conduce a los aiguiente:
1 q
X = ___ ( 1 - __________ )
2 So c Δx
| (8) |
en la cual q = caudal unitario; y So = pendiente promedio del lecho del canal.
Una forma conveniente de expresar los coeficientes de las Ecs. 5-7 es en términos de los números de Courant y de Reynolds de la celda. El número de Courant se define como:
y el número de Reynolds de la celda:
q
D = __________
So c Δx
| (10) |
Esto conduce a lo siguiente:
1 + C - D
C1 = _____________
1 + C + D
| (11) |
- 1 + C + D
C2 = _____________
1 + C + D
| (12) |
1 - C + D
C3 = _____________
1 + C + D
| (13) |
3. ENFOQUE CLÁSICO DEL MÉTODO MUSKINGUM
El enfoque clásico para la derivación del método Muskingum utiliza la ecuación de continuidad en su forma integrada espacialmente:
en las cuales I = caudal de entrada; O = caudal de salida; y V = volumen de almacenamiento en el tramo. Además, una función ponderada de entrada, salida y almacenamiento de la forma:
V = K [XI + ( 1 - X )O ]
| (15) |
se utiliza en lugar de la ecuación de cantidad de movimiento.
La solución de las Ecs. 14 y 15 en el plano discreto x-t conduce a la misma Ec. 4 que se obtuvo de la ecuación de onda cinemática, Ec. 3. La ecuación de onda cinemática se deriva de la ecuación de continuidad y una forma simplificada de la ecuación del momento que considera sólo el equilibrio de la gravedad y la fricción, de manera que:
en las cual Sf = pendiente de fricción. Por lo tanto, se deduce que la Ec. 15 es un análogo de la Ec. 16, en lugar de un análogo de la ecuación completa de movimiento.
4. EMBALSES LINEALES
El concepto de embalses lineales se ha utilizado ampliamente en relación con el modelado matemático de la escorrentía superficial. Es el proceso principal del modelo SSARR (9), que lo utiliza tanto en sus componentes de enrutamiento de cuencas como de canales. El método Kalinin-Milyukov de enrutamiento de inundaciones (4), desarrollado en la Unión Soviética, es otro método cuyo desarrollo se asemeja al del concepto de embalse lineal. Curiosamente, en el enrutamiento en canales, la suposición de un embalse lineal (Ec. 1) conduce a la llamada "longitud característica del tramo", tal como en el método Kalinin-Milyukov y desarrollos similares más recientes (7). La longitud característica del tramo Δxc se calcula especificando X = 0 en la Ec. 8:
La idea de una longitud característica de tramo asociada con el enrutamiento de canales, no se puede trasponer fácilmente al enrutamiento de cuencas. La complejidad del entorno de la cuenca impide la estimación de Δxc sobre la base de cantidades físicas medibles. Por lo tanto, si bien el concepto de embalse lineal se puede aplicar al enrutamiento de canales en un sentido predictivo, sólo se puede aplicar al enrutamiento de cuencas en un sentido de identificación.
5. ECUACIÓN DE ENRUTAMIENTO SSARR
La ecuación de enrutamiento SSARR es un caso particular del método Muskingum en el que el concepto de almacenamiento de tipo embalse se implementa estableciendo X = 0 (4). De las Ecs. 8 y 10, X = 0 implica que D = 1. Sustituyendo D = 1 en las Ecs. 11 a 13 conduce a lo siguiente:
C
C1 = C2 = _________
2 + C
| (18) |
y:
2 - C
C3 = ________
2 + C
| (19) |
Sustituyendo las Ec. 18 y 19 en la Ec. 4 se obtiene lo siguiente:
2C Qjn + Qjn+1 2 - C
Qj+1n+1 = (________) (_______________) + (___________) Qj+1n
2 + C 2 2 + C
| (20) |
Y reordenando:
2C Qjn + Qjn+1
Qj+1n+1 = (________) [(______________) - Qj+1n ] + Qj+1n
2 + C 2
| (21) |
la cual se reconoce como la ecuación de enrutamiento SSARR, debido a que el número de Courant C = c Δt /Δx = Δt /K = Δt /Ts.
6. CASCADA DE EMBALSES LINEALES
La Ecuación 21 se utiliza en el modelo numérico de la cascada de embalses lineales, tal como el modelo SSARR. El análisis de la Ec. 21 conduce a las siguientes conclusiones:
Para C > 2, es decir, el intervalo de enrutamiento excede al doble del tiempo de almacenamiento, hay un efecto de amplificación numérica;
Para C = 2, es decir, el intervalo de enrutamiento es igual al doble del tiempo de almacenamiento, el flujo de salida es igual al flujo de entrada promedio; y
Para 0 < C < 2, es decir, el intervalo de enrutamiento es menor que el doble del tiempo de almacenamiento, hay un efecto de difusión numérica. Debe tenerse en cuenta que la cantidad de difusión es una función del número de Courant, con los valores más pequeños de C resultando en un mayor efecto de difusión.
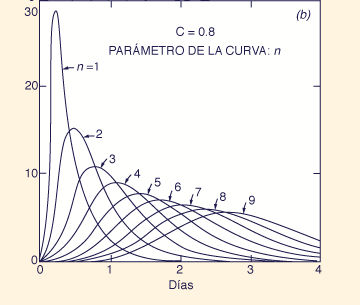
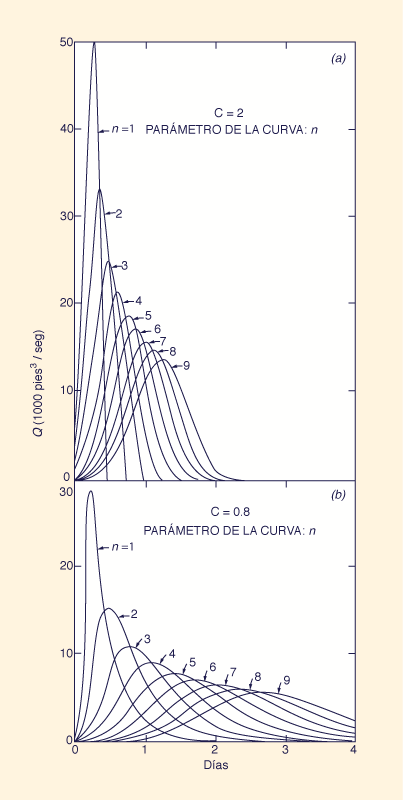
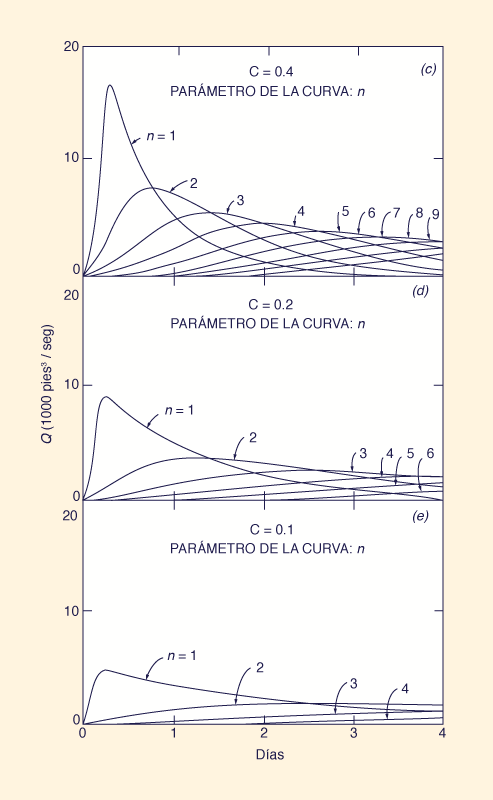
Fig. 2 Hidrogramas calculados en función del número de Courant C y el número de embalses lineales en serie n:
(a) C = 2.0; (b) C = 0.8; (c) C = 0.4; (d) C = 0.2; (e) C = 0.1.
La flexibilidad del modelo conceptual de la cascada de embalses lineales para modelar una amplia gama de eventos de escorrentía de cuencas se ilustra aplicando la Ec. 21 a una tormenta de 1 pulgada y de 6 h de duración, distribuida uniformemente sobre un área de 465 millas cuadradas (1,204 km2), lo que corresponde a un caudal de 50,000 cfs (1,416 m3/s). La Figura 2 muestra los hidrogramas calculados para una cascada de hasta nueve embalses lineales, correspondientes a números de Courant de 2.0, 0.8, 0.4, 0.2 y 0.1. El análisis de esta figura permite concluir los siguiente:
Para un número de Courant dado, un mayor número de embalses lineales da como resultado caudales máximos más pequeños y tiempos de retardo más largos.
Para un número dado de embalses, valores más pequeños del número de Courant dan como resultado caudales máximos más pequeños y tiempos de retardo más largos.
La La asimetría del hidrograma es una función del número de Courant. A medida que aumenta el número de Courant, disminuye el efecto de sesgo positivo (aumento rápido, descenso lento). A medida que el número de Courant tiende al valor C = 2, la asimetría desaparece.
La integración del área bajo los hidrogramas calculados muestra que el método conserva masa. No se han detectado ganancias o pérdidas de masa.
7. RESUMEN Y CONCLUSIONES
El modelo conceptual de la cascada de embalses lineales, en particular la ecuación de enrutamiento SSARR, se revisa a la luz de la teoría de difusión numérica. Se demuestra que la ecuación de enrutamiento SSARR es un caso especial de la ecuación de enrutamiento de Muskingum. Dado que este último simula los procesos de difusión "descentrando" la derivada temporal en su formulación discreta, se deduce que el mismo mecanismo de difusión numérica está contenida en la ecuación de enrutamiento SSARR y su supuesto asociado de embalse lineal. La extensión de la técnica a una cascada de embalses lineales, proporcionando así un parámetro adicional con fines de simulación, se prevé fácilmente.
En la práctica, el uso de un modelo conceptual como la cascada de embalses lineales continúa siendo un problema de identificación del sistema: dado los datos de entrada (precipitación efectiva) y la respuesta del sistema (caudal de salida), las características generales del sistema (los parámetros del modelo) se obtienen mediante calibración. En el caso de la ecuación de enrutamiento SSARR, los parámetros del modelo son el número de Courant, C, y el número de embalses, n. Una vez que se determinan los parámetros, se espera que puedan utilizarse en la etapa predictiva del modelado. En la medida en que esto se puede hacer, al menos aproximadamente (3, 10), el modelo conserva una estructura esencialmente lineal.
APÉNDICE I. BIBLIOGRAFÍA
-
Chow, V. T. 1974. Handbook of applied hydrology, McGraw-Hill Book Co., Inc., New York, N.Y..
-
Cunge, J, A. 1969. "On the subject of a flood propagation computation method (Muskingum method)," Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
-
Dodge, J. C. I. 1977. "Problems and methods of Rainfall-Runoff modeling," Mathematical Models for Surface Water Hydrology, T. A. Ciriani, V. Maione and J. R. Wallis, eds., John Wiley and Sons, London, England.
-
Miller, W. A., y J. A. Cunge. 1975. "Simplified equations of unsteady flow," Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publication, Fortn Collins, Colo., 1975, 183-257.
-
Nash, J. E. 1957. "On the norm of the instantaneous unit hydrograph," International Association for Scientific Hydrology, Publication No. 45, Vol. 3, pp. 110.121.
-
Ponce, V. M., y V. Yevjevich. 1978. "The Muskingum-Cunge method with variable parameters," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, Proc. Paper 14199, Dec.
-
Ponce, V. M. 1979. "Simplified Muskingum routing equation," Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY1, Proc. Paper 14275, Jan., 85-91.
-
Price, R. K. 1978. "A river catchment flood model," Proceedings of the Institution of Civil Engineers, London, England, Part 2, Vol. 65, Sept., 655-688.
-
Program Description and User Manual for SSARR Model, Streamflow Synthesis and Reservoir Regulation, U.S. Army Engineer North Pacific Division, Portland, Oreg., Sept., 1972, revised June, 1975.
-
Rao, R. A., J. W. Delleur, y B. S. Sarma. 1972. "Conceptual hydrologic models for urbanizing basins." Journal of the Hydraulics Division, ASCE, Vol. 98, No. HY7, Proc. Paper 9024, July, 1205-1220.
-
"WMO project on intercomparison of conceptual models used in operational hydrological forecasting," Mathematical Models for Surface Water Hydrology, T. A. Ciriani, V. Maione and J. R. Wallis, eds., John Wiley and Sons, London, England, 1977.
APÉNDICE II. SIMBOLOGÍA
En este artículo se utilizan los siguientes símbolos:
C = número de Courant, Ec. 9;
C1, C2 y C3 = coeficientes, Ecs. 5-7;
c = celeridad de la onda cinemática;
D = número de Reynolds de celda, Ec. 10;
I = caudal de entrada;
K = coeficiente de almacenamiento, parámetro de Muskingum (tiempo de viaje);
n = número de embalses, número de incrementos de almacenamiento;
O = caudal de salida;
Q = caudal;
q = caudal unitario;
Sf = pendiente de fricción;
So = pendiente de fondo del canal;
Ts = tiempo de almacenamiento;
t = variable tiempo;
V = tramo de almacenamiento;
X = parámetro de Muskingum (factor de ponderación);
x = variable de espacio;
Δx = longitud de tramo;
Δxc = longitud característica del tramo, Ec. 17;
Δt = intervalo de enrutamiento; y
Γ(n) = función gamma de argumento n.
Subíndices
j = índice de espacio; y
n = índice de tiempo.
|