en la cual Q = caudal; c = celeridad de la onda; q_L = flujo lateral; x = variable espacial; y t = variable temporal. Esta ecuación es aplicable al modelado de corrientes de flujo así como al flujo en canales y cunetas. Para aplicaciones de flujo superficial, la onda cinemática, expresada en términos del caudal unitario, está dada por lo siguiente ecuación:

en la cual q = caudal unitario; i = intensidad de lluvia efectiva; y los términos restantes han sido definidos anteriormente.

La celeridad de la onda cinemática se define como la pendiente de la curva de gasto, ya sea caudal-área (Q = αA^β ) en el caso de flujo de una corriente, o caudal unitario-profundidad de flujo (q = ad ^m ) para flujo superficial. En consecuencia, c = dQ/dA = β(Q/A) = βu, en el caso del caudal; e igualmente, c = m (q/d ) = mu, para flujo superficial, en el cual u = velocidad media. En los canales naturales, la celeridad de la onda cinemática se expresa alternativamente como c = (1/T ) (dQ/dy), en el cual T = ancho superior de la sección de canal, y y = tirante.

La Ecuación 1 (y por extensión, la Ec. 2) es una ecuación diferencial de primer orden; por lo tanto, puede describir la convección pero no la difusión, el cual es un proceso de segundo orden. En la práctica, esto significa que la ecuación de la onda cinemática puede describir el traslado de una onda de inundación, pero no su atenuación a medida que ésta se propaga corriente abajo. A pesar de que la Ec. 1 no puede describir la difusión, se reconoce que es una ecuación cuasi-lineal porque la celeridad de la onda cinemática es una función del caudal. Esto le da a las ondas cinemáticas la tendencia a cambiar de forma a medida que se propagan. Si la celeridad aumenta con el caudal, la cara delantera de la onda se empinará; contrariamente, si la celeridad disminuye con el caudal, la cara delantera de la onda se atenuará. En el flujo superficial y en el flujo de la corriente propiamente dicha, la tendencia es que la onda se empine; en el flujo de la corriente poco profunda fuera de la orilla, la tendencia es que la onda se atenúe.

3.  SOLUCIONES DE ONDA CINEMÁTICA

La solución de la Ec. 1 (o Ec. 2) se puede intentar de varias maneras. Las soluciones analíticas son posibles para los modelos lineales de las ecuaciones de gobierno [ver, por ejemplo, Lighthill y Whitham, 1955; y Ponce y Simons, 1977]. Estas soluciones describen la convección de una cantidad de flujo (Q o q) con la celeridad c en ausencia de difusión. Las soluciones numéricas son posibles utilizando ya sea el método de características o el de diferencias finitas. Los primeros trabajos sobre la onda cinemática utilizaron el método de características. En las aplicaciones de flujo superficial, la no linealidad (o más bien, la cuasi-linealidad) de los fenómenos generalmente conducen a un empinamiento de la onda y al eventual desarrollo de un choque cinemático. Un choque cinemático es una onda cinemática que se ha llegado a empinar hasta el punto en que su componente ascendente presenta una cara casi vertical, y eventualmente el flujo desarrolla una singularidad, perdiendo así su propiedad de ser gradualmente variado.

4.  DIFUSIÓN Y DISPERSIÓN NUMÉRICAS

Aunque las soluciones de ondas cinemáticas que utilizan el método de características son propensas al desarrollo de choques, aparentemente debido a su falta de difusión, las soluciones que utilizan el método de diferencias finitas muestran un comportamiento diferente. Las soluciones de diferencias finitas, en virtud de su naturaleza discreta, introducen cantidades apreciables de difusión y dispersión numéricas. Estos efectos interfieren con los efectos físicos, modificándolos (Abbott, 1976). Por ejemplo, en aplicaciones de flujo superficial, la difusión numérica tiene el efecto de contrarrestar la tendencia de la onda a empinarse, deteniendo así el desarrollo del choque y permitiendo que se mantenga y continúe el cálculo del flujo no permanente gradualmente variado.

La presencia de difusión y dispersión numéricas en una solución utilizando el método de diferencias finitas está en el centro de la controversia que rodea al modelo de onda cinemática. Un esquema numérico se caracteriza por sus gráficas o retratos de error, en amplitud y fase (Leendertse, 1967). La representación de amplitud describe la forma en que la amplitud de la onda numérica se aproxima a la amplitud de la onda física, y la desviación se interpreta como difusión numérica. La representación de fase describe la forma en que la fase de la onda numérica se aproxima a la fase de la onda física, y la desviación se interpreta como dispersión numérica. Ejemplos de retratos de amplitud y fase para problemas de convección están dados por Cunge (1969) y Ponce et al. (1979).

Las soluciones por diferencias finitas de la ecuación de onda cinemática exhiben cantidades variables de difusión y dispersión numéricas, dependiendo del tipo de esquema utilizado para discretizar la Ec. 1 (o Ec. 2). Los esquemas (totalmente) centrados son de segundo orden y no exhiben difusión numérica. Sin embargo, estos esquemas pueden exhibir alguna dispersión numérica para números de Courant diferentes de 1. (En la teoría de ondas cinemáticas, el número de Courant se define como la relación entre la celeridad física, es decir, la celeridad de la onda cinemática c, y la "celeridad de la malla discreta" Δx /Δt, con Δx = el incremento espacial, o paso espacial, y Δt = el incremento temporal, o paso temporal). Los esquemas descentrados son de primer orden, exhibiendo cantidades variables de difusión numérica, dependiendo del tamaño de Δx y Δt. Los incrementos más pequeños dan como resultado cantidades más pequeñas de difusión numérica, y la difusión numérica desaparece a medida que los incrementos se reducen a cero. Estos esquemas también exhiben cantidades variables de dispersión numérica para números de Courant diferentes de 1.

La difusión numérica surge debido a la omisión del término de segundo orden de la correspondiente expansión de la serie de Taylor de las diferencias finitas. La dispersión numérica surge debido a la omisión del término de tercer orden de la expansión de la serie de Taylor (Cunge, 1969; Ponce et al., 1979). Por lo tanto, en una aplicación típica, la difusión numérica suele ser de un orden de magnitud mayor que la dispersión numérica. En la práctica, esto significa que, por regla general, la mayor parte del error de las soluciones numéricas puede atribuirse a la difusión numérica. Las excepciones son los casos en los que el número de Courant es sustancialmente menor que 1, en cuyo caso la dispersión numérica puede crecer hasta el punto en que se compara en tamaño con la difusión numérica.

La difusión numérica se manifiesta como la difusión o atenuación del hidrograma calculado. Dado que la ecuación de onda cinemática no tiene difusión física incorporada, se deduce que una solución en diferencias finitas en realidad está simulando la difusión física a través de la difusión numérica. El hecho de que este último sea artificial e intrínsecamente relacionado con el tamaño de la malla se puede demostrar fácilmente resolviendo el mismo problema varias veces, cada vez reduciendo a la mitad los incrementos espaciales y temporales; véase, por ejemplo, Ponce (1986). Llevada a un límite práctico, esta prueba conduce a la eventual desaparición de la difusión numérica en cuestión, con el resultado aproximándose a la solución analítica de la onda cinemática. El reconocimiento de este hecho llevó al Servicio de Conservación de Suelos del USDA (hoy NRCS), a principios de la década de 1980, a retirar su método convexo de enrutamiento de inundaciones. El método convexo mostró una gran sensibilidad al tamaño de la malla, y la difusión numérica desaparecía a medida que este tamaño se reducía.

La dispersión numérica se manifiesta como dispersión; es decir, como el empinamiento o aplanamiento del componente ascendente del hidrograma calculado. En ciertos casos extremos, la dispersión numérica es responsable de las ondulaciones, o los (usualmente pequeños) valores negativos observados al principio o al final del hidrograma (Hjelmfelt, 1985). En la práctica, estos valores negativos son pequeños y desaparecen, junto con los otros rastros de dispersión numérica, cuando los intervalos de espacio y tiempo se seleccionan de tal manera que el número de Courant se aproxime a 1.

Dado que la difusión y dispersión numéricas son inherentes a la elección de los intervalos de espacio y tiempo (y su relación con respecto a la celeridad de la onda, o perturbación), el resultado de una solución en diferencias finitas de las Ecs. 1 o 2 depende del tamaño de la malla; es decir, el hidrograma de escorrentía calculado varía con la elección del tamaño de este tamaño. Por lo tanto, parece inútil intentar "calibrar" un modelo de onda cinemática variando un parámetro físico como la n de Manning para hacer coincidir los resultados calculados con los datos observados. Esta práctica equivale a ajustar curvas; en el mejor de los casos, es un buen modelo conceptual, pero no debe interpretarse como un modelo determinístico.

5.  MODELADO DE ONDAS DE DIFUSIÓN

En la práctica, los hidrogramas de escorrentía medidos y calculados muestran una cierta cantidad de difusión. Para simular correctamente esta difusión, es necesario extender la teoría de onda cinemática para abarcar la teoría de onda de difusión. Siguiendo a Hayami (1951) y Lighthill y Whitham (1955), la ecuación de onda de difusión se deriva despreciando los términos de inercia local, inercia convectiva y fuente-momento en la ecuación de movimiento, lo que lleva a la siguiente ecuación para el flujo en un canal:

y una ecuación similar para el flujo superficial:

con v = difusividad hidráulica, definida como sigue:

y S_o = pendiente del fondo; y los demás términos han sido definidos anteriormente. Las Ecs. 3 y 4 describen el movimiento de ondas cinemáticas con componente de difusión. A diferencia de sus contrapartes las Ecs. 1 y 2, las Ecs. 3 y 4 son ecuaciones diferenciales parabólicas de segundo orden y, por lo tanto, pueden describir la difusión física, con el coeficiente de difusión definido por la Ec. 5.

La ecuación de la onda de difusión se puede resolver analíticamente, lo que lleva a la solución de la analogía de difusión de Hayami para las ondas de avenida, o numéricamente, con la ayuda de un esquema de diferencias finitas para ecuaciones parabólicas, como el esquema de Crank-Nicolson (Crandall, 1956). Una tercera alternativa es extender la solución en diferencias finitas de la onda cinemática al ámbito de las ondas de difusión, haciendo coincidir las difusividades físicas y numéricas (Cunge, 1969; Dooge, 1973). La difusividad física es la difusividad hidráulica dada por la Ec. 5. La difusividad numérica es el coeficiente de difusión numérico del modelo de onda cinemática discretizada, es decir, el coeficiente del término de error principal (de segundo orden). Cuando se utiliza el esquema de Muskingum para modelar la onda cinemática, este método se denomina modelo de Muskingum-Cunge (Flood 1975; Ponce y Yevjevich, 1978).

El método Muskingum-Cunge tiene la ventaja significativa sobre los modelos de ondas cinemáticas convencionales en que el resultados es esencialmente independiente del tamaño de la malla (Ponce y Theurer 1982; Ponce, 1986). Por lo tanto, la calibración requiere sólo una pequeña modificación de los parámetros de fricción y de sección transversal, tales como el n de Manning y el exponente de la curva de gasto (ya sea β para el flujo en canales o m para el flujo superficial). Entonces, la elección de intervalos espaciales y temporales se basa únicamente en consideraciones de escala.

6.  APLICABILIDAD DE LAS ONDAS CINEMÁTICAS

El problema de la aplicabilidad de las ondas cinemáticas ha interesado tanto a investigadores como a profesionales. Aunque las ondas cinemáticas se utilizaron originalmente para simular los caudales de los ríos (Seddon, 1900), es en el campo del flujo superficial donde surgieron por primera vez las preguntas con respecto a su precisión y aplicabilidad. Entre estas contribuciones destaca la de Woolhiser y Liggett (1967), quienes identificaron el parámetro k definido de la siguiente manera:

para caracterizar la aplicabilidad de la onda cinemática a situaciones de flujo superficial. En la Ec. 6, S_o = pendiente de fondo; L_o = longitud del plano de flujo superficial; d_o = profundidad normal; y F_o = número de Froude basado en el flujo normal. El parámetro k se ha denominado número de flujo cinemático (Liggett, 1975). Este parámetro se puede utilizar como criterio para ayudar a determinar si la solución de onda cinemática es lo suficientemente precisa cuando se utiliza para resolver problemas de flujo superficial. Según Woolhiser y Liggett (1967), un valor de k ≥ 20 indica que el flujo es decididamente cinemático y, por lo tanto, puede utilizarse la ecuación de la onda cinemática. Más recientemente, sin embargo, Morris y Woolhiser (1980) han establecido que para números de Froude bajos, también es necesario que k F_o² ≥ 5, una condición compatible con el criterio de Woolhiser y Liggett (k ≥ 20) para el caso de F_o ≥ 0.5.

Ponce et al. (1978) utilizaron una solución analítica del conjunto de ecuaciones linealizadas (Lighthill y Whitham, 1955) para desarrollar criterios para la aplicabilidad de ondas cinemáticas y de difusión para el caso del flujo en canales abiertos. Ellos utilizaron perturbaciones sinusoidales al flujo medio, con L = longitud de onda; y T = período de onda. Para ondas cinemáticas, el criterio de Ponce et al. establece que para que la solución tenga una precisión del 95% después de un período de propagación, el período de onda adimensional debe ser mayor que 171. El período de onda adimensional τ está dado por la siguiente ecuación:

en el cual u_o = velocidad media del flujo; d_o = profundidad de flujo; y S_o = pendiente de fondo. Para aplicaciones prácticas, el período de onda T puede tomarse como el doble del tiempo de subida del hidrograma de avenida.

Para las ondas de difusión, el parámetro τ/F_o, en el cual F_o = número de Froude del flujo normal, es un mejor descriptor de la precisión del cálculo, teniendo en cuenta los errores de fase y de amplitud. El criterio de aplicabilidad para las ondas de difusión esta dado por la siguiente ecuación (Ponce et al., 1978):

en la cual g = aceleración de la gravedad; y los términos restantes han sido definidos anteriormente.

Ponce et al. (1978) confirmaron las conclusiones de Lighthill y Whitham (1955), así como las de varias otras personas, que la mayoría de las situaciones de flujo superficial satisfacen el criterio de onda cinemática, y que la mayoría de los casos de propagación de ondas de inundación en canales (excluyendo aquéllos con un control significativo aguas abajo) satisfacen el criterio de onda de difusión. Sólo en situaciones con tendencias disipativas marcadamente fuertes (por ejemplo, una onda de inundación que se produce con la rotura de una presa); el flujo hacia grandes embalses (con efectos de remanso considerables); o inversiones en la dirección de flujo, sería necesario recurrir a la onda dinámica para describir adecuadamente la propagación de las ondas.

7.  FLUJO SUPERFICIAL VERSUS HIDROGRAMA UNITARIO

El problema de si una solución de onda cinemática de flujo superficial puede reemplazar (y quizás eventualmente retirar) el hidrograma unitario como un método práctico de generación de escorrentía continúa siendo un tema controversial. Debido a las diferencias fundamentales entre estos dos métodos, no parece que se llegue a una resolución de este conflicto en un futuro cercano. La solución de onda cinemática del flujo superficial es un método determinístico, de parámetros distribuidos, el cual hace uso extensivo de datos hidráulicos (parámetros geométricos y de fricción). La onda cinemática es principalmente aplicable a pequeñas cuencas (menores a 2.5 km²); para laa cuales las idealizaciones inherentes a la modelización matemática pueden justificarse sobre bases prácticas. En otras palabras, para que la solución de onda cinemática sea útil, la discretización debe reflejar lo que realmente está ocurriendo en el terreno. Cuando se usa indiscriminadamente, sin tener en cuenta la escala del problema, existe el riesgo de que la cantidad de agrupamiento introducido pueda interferir con el carácter determinístico del método y su capacidad para simular flujos superficiales en un contexto distribuido.

En contraste con la solución de onda cinemática de flujo superficial, el hidrograma unitario es un modelo conceptual de generación de escorrentía, agrupado espacialmente y basado exclusivamente en datos hidrológicos (mediciones de aforos). Aunque originalmente se derivó para grandes cuencas hidrográficas (Sherman, 1932), se ha encontrado que el método tiene aplicabilidad primordial para cuencas medianas, es decir, aquéllas mayores a 2,5 km² pero menores a 1000 km². Si bien estos límites son hasta cierto punto arbitrarios, tienden a reflejar la práctica actual de la ingeniería hidrológica. Además, en el contexto de un modelado adecuado (es decir, con la subdivisión de cuencas hidrográficas), la aplicabilidad del hidrograma unitario se extiende efectivamente a cuencas grandes.

Dado que la solución de onda cinemática de flujo superficial es principalmente aplicable a cuencas pequeñas, y que el hidrograma unitario se aplica principalmente a cuencas medianas (y, por extensión, a las grandes), parece que debería haber poca superposición entre estos dos métodos. En la práctica, sin embargo, los modelos existentes [por ejemplo, el modelo HEC-1 del Cuerpo de Ingenieros del Ejército de EE. UU. (HEC-1, 1985)] permiten a los usuarios la posibilidad de elegir entre estos dos métodos para resolver problemas de escurrimiento, independientemente de la escala. Esto lleva a la pregunta de cuál de los métodos es mejor o más preciso para un problema dado, un problema que no tiene una respuesta fácil. Los métodos son de naturaleza tan diferente y tienen necesidades de datos tan diferentes que no son fácilmente comparables. Quizás el único argumento defendible a este respecto es que la solución de onda cinemática debería aumentar en precisión a medida que disminuye el tamaño de la cuenca; y el hidrograma unitario debería aumentar en practicidad a medida que aumenta el tamaño de la cuenca. Es probable que las comparaciones específicas entre los dos métodos den lugar a discusiones acaloradas, pero no parece probable que el problema central de precisión se resuelva pronto. Por un lado, la solución de onda cinemática del flujo superficial se basa en el conocimiento imperfecto de los mecanismos de fricción, incluida la estimación del n de Manning y del exponente m de la curva que describe el régimen mixto laminar-turbulento que caracteriza la mayoría de las situaciones de flujo superficial. Asimismo, el hidrograma unitario tendría que verificarse con datos concurrentes de lluvia-escorrentía, los cuales no están fácilmente disponibles en los casos de cuencas de tamaño mediano.

Teniendo en cuenta el problema de la escala, la solución de onda cinemática tiene la ventaja significativa de que puede describir variaciones espaciales y/o temporales de precipitación y rugosidad, lo que el método del hidrograma unitario, en virtud de ser agrupado, no puede hacer. Por lo tanto, en situaciones en las que el problema de la escala pueda minimizarse, la solución del flujo superficial debería proporcionar un mayor detalle en la simulación de flujos de inundación, incluida la descripción de los procesos de concentración y difusión de la escorrentía. Allí radica la promesa de las ondas cinemáticas y la expectativa de mejoras significativas en la precisión del cálculo.

A medida que las soluciones de ondas cinemáticas continúen madurando, particularmente con el advenimiento de una descripción físicamente significativa de la difusión de la escorrentía, se allanará el camino para que los dos métodos se complementen entre sí. Existe una necesidad imperiosa de desarrollar hidrogramas unitarios sintéticos que vayan más allá de la práctica establecida [el hidrograma unitario de Snyder, para seguir la práctica del Cuerpo de Ingenieros; o el hidrograma adimensional NRCS, para seguir al Servicio de Conservación de Recursos Naturales, (USDA: SCS 1985)]. Actuando sobre esta necesidad, la Oficina de Recuperación de Tierras de los EE. UU. ha desarrollado un conjunto de hidrogramas unitarios sintéticos regionales para su uso dentro de su jurisdicción (11 estados del Oeste de los Estados Unidos) (USBR: Design 1987). En un intento por superar las deficiencias de los hidrogramas unitarios sintéticos convencionales, las agencias locales se dedican a desarrollar hidrogramas unitarios sintéticos del tipo hidrograma S (Sabol 1987, 1990). Se prevé que, en el contexto de un modelado adecuado, el modelo de onda cinemática de flujo superficial se puede utilizar como una herramienta para desarrollar hidrogramas unitarios sintéticos prescindiendo de una red extensa (y costosa) de colección de datos de flujo (ver Overton, 1970).

Un precedente para el uso de modelos para sintetizar los caudales máximos ya existe en la práctica hidrológica estadounidense: el método TR-55 (USDA: "Urban" 1986). Este método NRCS de generación de flujos pico se desarrolló utilizando el modelo de cuenca TR-20 (USDA: "Computer" 1983) para generar flujos picos sintéticos tomando en cuenta las propiedades de concentración de la cuenca, la distribución temporal regional de la lluvia y los mecanismos de infiltración y de almacenamiento de las depresiónes. El método TR-55 mejora el método racional, sustituyendo el modelado por el empirismo, y conduciendo a mejores y más consistentes predicciones de escurrimiento.

8.  CHOQUE CINEMÁTICO

El choque cinemático fue tratado en detalle por Lighthitll y Whitham (1955); y desde entonces, varios estudios se han esforzado por analizar sus causas y efectos. Aún así, el tema continúa desconcertando a investigadores y profesionales por igual (Cunge, 1969; Kibler y Woolhiser, 1970). El choque surge debido a la característica no lineal de las ondas cinemáticas, la cual bajo las condiciones apropiadas, puede resultar en que la onda cinemática se empine hasta el punto en que pueda convertirse, para todos los propósitos prácticos, en una muralla de agua. (En situaciones de flujo superficial, la "muralla de agua" sería una pequeña discontinuidad en el perfil de la superficie del flujo). El choque es una consecuencia directa de la tendencia no lineal a empinarse, que es promovida bajo las condiciones detalladas en el cuadro adjunto (Ponce y Windingland, 1985)

Primero, la onda es cinemática, en oposición a difusiva (o dinámica). La difusión es un mecanismo que actúa para oponerse a la tendencia no lineal de empinamiento. Cuanto más difusiva (o dinámica) es una onda, menos cinemática es y, por lo tanto, menor es la tendencia al empinamiento. Segundo, existe una baja relación de flujo base a flujo pico. La tendencia a empinarse se promueve cuando el flujo está sujeto a grandes cambios relativos, es decir, cuando el flujo base es sólo una pequeña fracción del flujo pico. En el límite, cuando el caudal base se acerca a cero, es decir, en el caso de un arroyo efímero, la tendencia a empinarse (debido a esta condición) se promueve. Esto explica el hecho de que el choque es una ocurrencia relativamente más frecuente en el caso de inundaciones repentinas en regiones áridas y semiáridas, las cuales son causadas por tormentas intensas que concentran grandes caudales en lechos fluviales efímeros. Tercero, el canal o corriente es hidráulicamente ancho y suficientemente largo. Dado que la pendiente de la onda es gradual, se necesita un canal suficientemente largo para que el choque tenga la oportunidad de desarrollarse. Las tendencias fuertes de empinamiento pueden requerir una longitud más corta; es posible que una tendencia débil nunca llegue a desarrollar el choque, dado el efecto de los flujos laterales entrantes, los cuales tienden a recomenzar (resetear) el proceso. Una condición necesaria para el desarrollo del choque es que el canal sea hidráulicamente ancho, es decir, uno en el cual el perímetro mojado sea casi constante. En la práctica, esta condición hidráulica se refleja en una situación geomorfológica tipo cañón, con paredes esencialmente verticales en las que a medida que aumenta el flujo, el perímetro mojado aumenta muy poco en comparación con el aumento en la profundidad y área del flujo. Matemáticamente, esta condición está representada por un exponente de la curva de gasto β mucho mayor que 1 (aproximándose a β = 3/2 para la fricción de Chezy; o β = 5/3 para la fricción de Manning). Por otro lado, en situaciones de flujo poco profundo sobre la orilla (con canales que expanden rápidamente su sección transversal, de modo que el perímetro mojado aumenta en la misma proporción que el área de flujo y, en consecuencia, el radio hidráulico permanece casi constante), la tendencia a empinarse se contrarresta y el choque no se desarrolla. Matemáticamente, esta condición está representada por un valor del exponente de la curva de gasto que contrarresta la tendencia al empinamiento y detiene el desarrollo del choque. Matemáticamente, esta condición está representada por un valor del exponente de la curva de gasto β ≅ 1. Cuarto, el flujo tiene un alto número de Froude. En canales hidráulicamente anchos, los flujos con alto número de Froude carecen de difusión suficiente para contrarrestar eficazmente la tendencia a empinarse (Ponce y Simons, 1977). Por lo tanto, para números de Froude altos, cerca al tirante crítico o por encima de él, la tendencia a empinarse puede promoverse hasta el punto en que el choque puede desarrollarse debido a esta condición. En teoría, a medida que el número de Froude para flujo turbulento se aproxima a la condición de estabilidad neutra (Fn = 1.5 para fricción de Manning; Fn = 2 para la fricción de Chezy), el choque se vuelve inestable y la teoría ya no es aplicable. En la práctica, sin embargo, estos flujos con alto número de Froude son raros en los ríos y cursos naturales, y la inestabilidad rara vez se observa. Sin embargo, en los canales artificiales y de otro tipo, con recubrimientos relativamente poco rugosos, la inestabilidad de la superficie libre conduce a las reconocidas ondas pulsantes o de rollo (Dressler, 1949; Chow 1959; Jolly y Yevjevich, 1971). Estas ondas de rollo se observan a menudo en calles empinadas y situaciones similares donde las condiciones predominantes de flujo laminar (o mixto laminar-turbulento) pueden reducir el número de Froude para la estabilidad neutra a valores muy por debajo del correspondiente al flujo turbulento (Fn ≅ 1 para flujo mixto laminar-turbulento; y Fn = 0.5 para flujo laminar propiamente dicho).

Las cuatro condiciones físicas anteriores contribuyen al desarrollo del choque. Cuando todas ocurren al mismo tiempo, es muy probable que se desarrolle el choque. Si sólo uno o dos de ellas están presentes, es posible que el choque no se desarrolle. Si bien el choque cinemático ha sido interpretado de manera diferente por varios autores [véanse, por ejemplo: Cunge, 1969 y Kibler y Woolhiser, 1970], no hay duda de que el choque es físico y que ocurre bajo el conjunto adecuado de circunstancias altamente oportunas. Desafortunadamente, en la literatura se carece de documentación adecuada de la ocurrencia de choques cinemáticos. 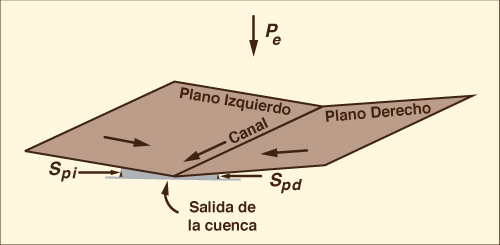Las mediciones son casi imposibles, y los avistamientos son todo lo que los observadores diligentes pueden esperar. El impacto parece estar presente en inundaciones repentinas, siendo la inundación asesina una manifestación nefasta del choque cinemático [véase, por ejemplo: el relato de Hjalmarson sobre la inundación del 26 de julio de 1982 en el arroyo Tanque Verde, al este de Tucson, Arizona, en el cual las vidas de ocho bañistas desprevenidos se cobraron por lo que, en toda probabilidad, fue un choque cinemático (Hjalmarson, 1985)].

Habiendo sido identificadas las condiciones para el desarrollo del choque cinemático, queda la pregunta de si el choque cinemático es tan común en la práctica como parecieran indicar los cálculos que utilizan un modelo de onda cinemática de flujo superficial. Por ejemplo, el choque es una ocurrencia común en soluciones de ondas cinemáticas usando el método de las características. Esto es comprensible, ya que este método resuelve la ecuación de onda cinemática sin introducir difusión numérica. Un ejemplo: Kibler y Woolhiser (1970) utilizaron el método de las características para estudiar la cascada de planos como un posible modelo hidrológico, y pudieron derivar un parámetro de choque cinemático en función de las características geométricas y de fricción de dos planos adyacentes. Sin embargo, al resumir sus hallazgos, Kibler y Woolhiser observaron lo siguiente:

"Si bien el choque cinemático puede surgir bajo ciertas circunstancias físicas altamente selectivas, en este estudio se considera como una propiedad de las ecuaciones matemáticas utilizadas para explorar el problema del flujo superficial más que como una característica observable de este proceso hidrodinámico".

El choque es una ocurrencia mucho menos común en soluciones de diferencias finitas, particularmente cuando éstas presentan un componente sustancial de difusión numérica. Por ejemplo, el choque está notoriamente ausente en el método convexo, que al descentrar completamente sus derivadas (de tiempo y espacio) presenta una cantidad considerable de difusión numérica (Ponce et al., 1979). Las soluciones características satisfacen intrínsecamente la primera condición antes mencionada; las soluciones en diferencias finitas generalmente no lo hacen. Sin embargo, como lo muestran Ponce y Windingland (1985), el choque puede de hecho desarrollarse en soluciones de diferencias finitas, particularmente cuando las cuatro condiciones se cumplen al mismo tiempo.

En la práctica, el choque es algo poco común en los canales naturales. En situaciones de flujo superficial, la presencia de choques se ha documentado bajo circunstancias altamente selectivas, generalmente en conexión con flujo superficial en planos rectangulares largos de pendiente constante (como las escorrentías intensas en calles empinadas y estacionamientos). Las irregularidades espaciales de las precipitaciones y las pequeñas irregularidades topográficas suelen generar suficientes efectos de difusión como para contrarrestar el desarrollo del choque. Por lo tanto, la presencia del choque en una solución de ondas cinemáticas, con más frecuencia de lo que se justifica (como en una solución característica), debe interpretarse como la incapacidad del método para tener en cuenta adecuadamente las irregularidades del flujo y en la cuenca de captación. Por lo tanto, la preferencia práctica por soluciones de diferencias finitas de ondas cinemáticas, donde el choque es una ocurrencia poco común, no es una gran sorpresa (Alley y Smith, 1982).

La resolución de este conflicto parece estar en la descripción adecuada de la difusión de la escorrentía dentro del contexto de una solución de onda cinemática sensu lato. La difusión contrarrestará eficazmente la tendencia al empinamiento no lineal, la cual es la causa principal del choque. Una mejor formulación de onda cinemática conducirá solo a casos aislados de la presencia del choque y, por lo tanto, estará mucho más de acuerdo con la realidad física.

9.  EXTENSIÓN DINÁMICA PARA ONDAS CINEMÁTICAS

Bajo un adecuado conjunto de supuestos de linealización, la teoría de ondas cinemáticas puede extenderse al ámbito de las ondas dinámicas (Ponce, 1990). Dooge (1973) derivó la expresión de la difusividad hidráulica dinámica ν_d , para el caso de un canal hidráulicamente ancho con fricción de Chezy:

Para el flujo superficial, una expresión general de la difusividad hidráulica dinámica es:

que se reduce a la Ec. 9 para m = 3/2.

Para el flujo en canales, una expresión de la difusividad hidráulica dinámica es (Ponce, 1986):

Dado que la difusividad hidráulica desaparece en la condición de estabilidad neutra, las Ecs. 9-11 explican el comportamiento dinámico de las ondas (Ponce y Simons, 1977). Esta condición se caracteriza por el número de Vedernikov V = 1. El número de Vedernikov (Vedernikov, 1945; Powell, 1948; Craya, 1952; Chow, 1959) es:

Dadas las Ecs. 10-12, la difusividad hidráulica dinámica se puede expresar en términos del número de Vedernikov de la siguiente manera:

Para β = 1 [es decir, un canal de ancho superior que se expande rápidamente de manera que el perímetro mojado aumenta en la misma proporción que el área de flujo (un canal de radio hidráulico constante)], la Ec. 12 predice que V = 0, y la difusividad hidráulica dinámica (Ec. 13) se reduce a la difusividad hidráulica de la Ec. 5. Esto confirma la observación práctica de que el choque cinemático casi no ocurre en un canal con un exponente de la curva de gasto β ≅ 1.

Dada la Ec. 13, es posible extender la teoría de ondas cinemáticas al ámbito de las ondas dinámicas. De seta manera, un componente dinámico puede incorporarse de manera efectiva en las soluciones de flujo superficial, mientras permanece dentro del mismo marco computacional de las soluciones de ondas cinemáticas. El uso de una difusividad hidráulica dinámica (es decir, dependiente del número de Vedernikov) está destinado a ser más general que las soluciones de onda cinemática o de difusión, particularmente en situaciones en las que el número de Vedernikov es sustancialmente diferente de cero (por ejemplo, para flujos cerca al crítico y supercríticos dentro del banco u orilla). Sin embargo, su viabilidad cuando se aplica a problemas de flujo superficial queda por determinar mediante un estudio más detallado.

10.  RESUMEN Y CONCLUSIONES

Se revisan la teoría de las ondas cinemáticas y de difusión, impulsadas por la continua controversia referente a su naturaleza y aplicabilidad. Se demuestra que las ondas cinemáticas no son difusivas, pero que sufren cambios de forma durante la propagación debido a su naturaleza no lineal. En el flujo superficial y en el flujo en canales (dentro del banco), esta característica le da a las ondas cinemáticas la capacidad de empinarse, lo cual eventualmente conduce a la formación del choque cinemático. Se demuestra que el choque cinemático es poco común y que ocurre solo bajo un conjunto de circunstancias altamente selectivas, que incluyen: (1) Una onda cinemática propiamente dicha; (2) una relación pequeña de flujo base a flujo pico; (3) un canal hidráulicamente ancho y suficientemente largo; y (4) un flujo con alto número de Froude. La ocurrencia común del choque cinemático en soluciones de flujo superficial, particularmente cuando se usa el método de las características, se atribuye a la ausencia total de difusión del escurrimiento en estas soluciones. En la práctica, las pequeñas irregularidades en el flujo y geomorfología de la cuenca suelen producir suficientes efectos difusivos para contrarrestar el desarrollo del choque.

Se ha demostrado que las soluciones de ondas cinemáticas que utilizan diferencias finitas poseen cantidades intrínsecas de difusión y dispersión numéricas, como consecuencia del tamaño finito de la malla. Estos efectos numéricos son artificiales y tienden a desaparecer a medida que se refina (reduce) el tamaño de la malla. En el límite, cuando el tamaño de la malla se aproxima a cero, los efectos numéricos tienden a desaparecen. En la práctica, esto significa que las soluciones de ondas cinemáticas de flujo superficial dependen de la malla; es decir, los resultados son función del tamaño de ésta, con la solución típica presentando cantidades apreciables de difusión y dispersión numéricas.

El modelado de ondas cinemáticas se puede mejorar ampliando la teoría de ondas cinemáticas al ámbito de las ondas de difusión. De esta manera, la difusión inherente en los cálculos prácticos de escorrentía puede calcularse directamente en el modelado. En este sentido, el método Muskingum-Cunge es particularmente atractivo, porque si bien se mantiene dentro del marco computacional de los modelos de ondas cinemáticas, tiene suficiente información física para comparar favorablemente con soluciones numéricas implícitas de la ecuación de la onda de difusión. A diferencia de los modelos convencionales de ondas cinemáticas de diferencias finitas, el resultado del método Muskingum-Cunge es independiente del tamaño de la malla, lo que enfatiza aún más su utilidad como modelo práctico de la onda difusiva.

Se revisa la aplicabilidad de las ondas cinemáticas y difusivas. Se concluye, haciéndo eco de estudios anteriores, que la mayoría de las situaciones de flujo superficial satisfarían el criterio de onda cinemática, y que la mayoría de los casos de propagación de ondas de crecida en canales o corrientes cumplirían el criterio de onda de difusión. Sólo en situaciones con tendencias disipativas fuertes o un control sustancial aguas abajo sería necesario recurrir a la onda dinámica para describir adecuadamente la propagación de ondas poco profundas.

El problema de la elección entre los métodos de onda cinemática e hidrograma unitario para cálculos prácticos de escurrimiento se examina con la ayuda del concepto de escala de la cuenca. El uso del método de onda cinemática está indicado principalmente para cuencas pequeñas (menores a 2.5 km²), particularmente en los casos en los cuales es posible resolver el detalle físico sin comprometer la naturaleza determinística del modelo. Se recomienda el uso del método del hidrógrama unitario para cuencas de tamaño mediano; es decir, mayores a 2.5 km² y menores a 1,000 km², para los cuales el método de la onda cinemática puede resultar difícil de implementar. Se recomienda el uso de la onda cinemática como herramienta para el desarrollo de hidrogramas unitarios sintéticos.

Se revisa la extensión dinámica a la teoría de ondas cinemáticas y de difusión con miras al futuro. Se demuestra que la extensión dinámica tiene en cuenta adecuadamente la dependencia de la difusividad hidráulica del número de Vedernikov, lo que permite que la simulación sea compatible con el efecto dinámico. Este tipo de modelado sería particularmente aplicable al flujo en canales para el cual el número de Vedernikov sea sustancialmente diferente de cero; por ejemplo, para flujos cercanos al crítico y flujos supercríticos limitados dentro del banco u orilla.

APÉNDICE I.  REFERENCIAS BIBLIOGRÁFICAS

Abbott, M. B. 1976. "Computational hydraulics: A short pathology." J. Hydr. Res., 14(4), 271-285.

Alley, W. M., y P. E. Smith. 1982. "Distributed routing rainfall-runoff model ^___ version II: User's manual." Open-File Report 82-344, U.S. Geological Survey Water Resources Division, Gulf Coast Hydroscience Center, NSTL Station, Miss.

Chow, V. T. 1959. Open-channel hydraulics. McGraw Hill Book Co., Inc., New York, N.Y.

"Computer program for project formulation-hydrology." 1983. USDA Soil Conservation Service, Tech. Release No. 20 (TR-20), Washington, D.C.

Cunge, J. A. 1969. "On the subject of a flood propagation computation method (Muskingum method)." J. Hydr. Res., 7(2), 205-230.

Crandall, S. H. 1956. Engineering analysis: A survey of numerical procedures. McGraw-Hill Book Co., New York, N.Y.

Craya, A. 1952. "The criterion for the possibility of roll wave formation." Proc., Gravity Waves Symp., Circular 521, U.S. National Bureau of Standards, Washington, D.C., 294-332.

Dawdy, D. R. 1990. Discussion of "Kitthmatic wave routing y computational errror." J. Hydr. Engrg., ASCE, 116(2), 278-280.

Design of Small Dams. 1987. U.S. Bureau of Reclamation, Denver, Colorado, 3rd ed.

Dooge, J. C. I. 1973. "Linear theory of hydrologic systems." Tech. Bulletin No. 1468, USDA Agricultural Research Service, Washington, D.C.

Dressler, R. F. 1949. "Mathematical solution of the problem of roll waves in inclined open channels." Communications in Pure y Appl. Mathematics, 2, 149-194.

Flood Studies Report. 1975. Natural Environment Research Council, London, England, Vol. III.

Goldman, D. 1990. Discussion of "Kinematic wave routing y computational error." J. Hydr. Engrg., ASCE, 116(2), 280-282.

Hayami, S. 1951. "On the propagation of flood waves." Bulletin of the Disaster Prevention Research Institute, Disaster Prevention Research Institute, Kyoto, Japan, 1(1), 1-16.

HEC-1, Flood Hydrograph Package: Users' Manual. 1985. U.S. Army Corps of Engineers, Hydrologic Engineering Center, Davis, Calif.

Hjalmarson, H. W. 1984. "Flash flood is Tanque Verde Creek, Tucson, Arizona," J. Hydr. Engrg., 110(12), 1841-1852.

Hjelmfelt, A. T. 1984. "Negative outflows from Muskingum flood routing." J. Hydr. Engrg., ASCE, 111(6), 1010-1014.

Hromadka, T. V., y J. J. DeVries. 1988. "Kinematic wave y computational error." J. Hydr. Engrg., ASCE, 114(2), 207-217.

Hromadka, T. V., y J. J. DeVries. 1990. Closure of "Kinematic wave y computational error." J. Hydr. Engrg., ASCE, 116(2), 288-289.

Jolly, P. J., y V. Yevjevich. 1971. "Amplification criterion of gradually varied, single peaked waves." Hydrol. Paper No. 51, Colorado State University, Fort Collins, Colo.

Kibler, D. F., y D. A. Woolhiser. 1970. "The kinematic cascade as a hydrologic model." Hydrol. Paper No. 39, Colorado State University, Fort Collins, Colo.

Leendertse, J. J. 1967. "Aspests of a computational model for long-period water wave propagation." RM.5294.PR, The Rand Corporation, Santa Monica, Calif.

Liggett, J. A. 1975. "Basic equations of unsteady flow." Unsteady flow in open channels, K. Mahmood y V. Yevjevich, eds., Water Resources Publications. Fort Collins, Colo., Vol. 1.

Lighthill, M. J., y G. B. Whitham. 1955. "On kinematic waves. I: Flood movement in long rivers." Proc., Royal Society, London, England, A229, 281-316.

Merkel, W. H. 1990. Discussion of "Kinematic wave routing y computational error." J. Hydr. Engrg., ASCE, 116(2), 282-284.

Morris, E. M., y D. A. Woolhiser. 1980. "Unsteady one-dimensional flow over a plane: Partial equilibrium y recession hydrographs." Water Resour. Res., 16(2), 355-360.

Overton, D. E. 1970. "Route o Convolute?" Water Resour. Res., 6(l), 43-52.

Ponce, V. M., y Simons, D. B. 1977. "Shallow wave propagation in open channel flow." J. Hydr. Div., ASCE, 103(12), 1461-1476.

Ponce. V. M., R. M. Li, y D. B. Simons. 1978. "Applicability of kinematic y diffusion models." J. Hydr. Div., ASCE, 104(3), 353-360.

Ponce, V. M., y Yevjevich, V. 1978. "Muskingum-Cunge method with variable parameters." J. Hydr. Div., ASCE, 104(12), 1663-1667.

Ponce, V. M., Y. H. Chen, y D. B. Simons. 1979. "Unconditional stability in convection computations." J. Hydr. Div., ASCE, 105(9), 1079-1086.

Ponce, V. M., y F. D. Theurer. 1982. "Accuracy criteria in diffusion routing." J. Hydr. Div., ASCE, 108(6), 747-757.

Ponce, V. M., y D. Windingland. 1985. "Kinematic shock: Sensitivity analysis." J. Hydr. Engrg., ASCE, 111(4), 600-611.

Ponce, V. M. 1986. "Diffusion wave modeling of catchment dynamics." J. Hydr. Engrg., ASCE, 112(8), 716-727.

Ponce, V. M. 1990. "Generalized diffusion wave model with inertial effects." Water Resour. Res., 26(5). 1099-1101.

Powell, R. W. 1948. "Vedernikov criterion for ultrarapid flow." Transactions, American Geophysical Union, 29(6), 882-886.

Sabol, G. V. 1987. "Development, use, y synthesis of S.graphs." Proc., Engrg. Hydrol. Symp., ASCE. New York, N.Y., 627-632.

Sabol". G. V. 1990. "Maricopa County Hydrology Procedure." Proc., Watershed Management Symp., ASCE, New York, N.Y., 423-431.

SCS National Engineering Handbook, Section 4: Hydrology. 1985. USDA Soil Conservation Service, Washington, D.C.

Seddon, J. A. 1900. "River hydraulics." Trans., ASCE, 43, 179-229.

Sherman, L. K. 1932. "Streamflow from rainfall by unit-graph method." Engrg. News Record, 108, April 7, 501-505.

Unkrich, C. L., y D. A. Woolhiser. 1990. Discussion of "Kinematic wave routing y computational error." J. Hydr. Engrg., ASCE, 116(2), 284-286.

"Urban Hydrology for Small Watersheds." 1986. Tech. Release No. 55 (TR-55), USDA Soil Conservation Service, Washington, D.C.

Vedernikov, V. V. 1945. "Conditions at the front of a translation wave distributing a steady motion of a real fluid." Comptes Rendus (Doklady) de l'Academie des Sciences de l' U.R.S.S., (in French), 48(4).

Woolhiser, D. A., y J. A. Liggett. 1967. "Unsteady one-dimensional flow over a plane-the rising hydrograph." Water Resour. Res., 3(3), 753-771.

Woolhiser, D. A., y D. C. Goodrich. 1990. Discussion of "Kinematic wave routing y computational error." J. Hydr. Engrg., ASCE, 116(2), 278-288.

APÉNDICE II.  NOTACIÓN