en la cual Δt = intervalo de tiempo para el enrutamiento. En la versión Muskingum-Cunge, los parámetros K y X se calculan con las siguientes fórmulas (2,3,4);

Δx K  =  _____            c

(6)

1                   q    X  =  ___ ( 1  -  __________ )           2              So c Δx

(7)

en las cuales Δx = longitud de tramo (intervalo de espacio); c = celeridad de la onda de inundación; q = descarga por unidad de ancho; y S_o = pendiente de fondo del canal. Sustituyendo las Ecs. 6 y 7 en las Ecs. 3-5:

1 + C - D C1  =  ______________              1 + C + D

(8)

-1 + C + D C2  =  _______________              1 + C + D

(9)

1 - C + D C3  =  ______________              1 + C + D

(10)

en la cual C = c Δt /Δx es el número de Courant; y D = (q /S_o)/cΔx es un tipo de número de Reynolds de la célula. Tanto C como D tienen importancia física y numérica, siendo C una razón de celeridades y D una razón de difusividades.

3.  PARáMETROS VARIABLES

Usualmente, Δt es fijo, y Δx y S_o se especifican para cada celda computacional que consta de cuatro puntos adyacentes en la malla (dos en el espacio y dos en el tiempo) (Fig. 1). Por lo tanto, es necesario determinar la celeridad de la onda de inundación, c, y la descarga por ancho de unidad, q, para cada celda computacional. Los valores de c y q en los puntos de la malla (j, n) son definidos por:

dQ c  =  _____           dA

(11)

Q q  =  _____            B

(12)

en la cual Q = descarga; A = area de flujo; y B = ancho superior. Las siguientes formas de determinar c y q para su uso en el cálculo de C y D son concideradas:

1. Directamente, mediante el uso del promedio de los valores en los puntos de la malla (j, n) y (j + 1, n);

2. Directamente, mediante el uso del promedio de los valores en los puntos de la malla (j, n), (j + 1, n), y (j, n + 1); y

3. Mediante iteración, con un cálculo utilizando cuatro puntos. Para mejorar la convergencia, los valores en (j + 1, n + 1) obtenidos por el método de los tres puntos son usados como primera estimación de la iteración.

4.  EJEMPLO

El método Muskingum-Cunge con parámetros variables se aplica aquí al problema planteado por Thomas (8) en su artículo clásico sobre el enrutamiento de avenidas. El problema consiste en calcular la translación y la atenuación de la onda de inundación de forma sinusoidal en un canal de ancho unitario con una curva de gasto (flujo permanente) dada por la siguiente ecuación:

q  =  0.688 d  5/3

(13)

El hidrograma de entrada se define en la siguiente forma:

π t I(t)  =  125 - 75 cos ( ____ ),          0 ≤ t ≤ 96;                                       48

(14a)

I(t) = 50,          t > 96

(14b)

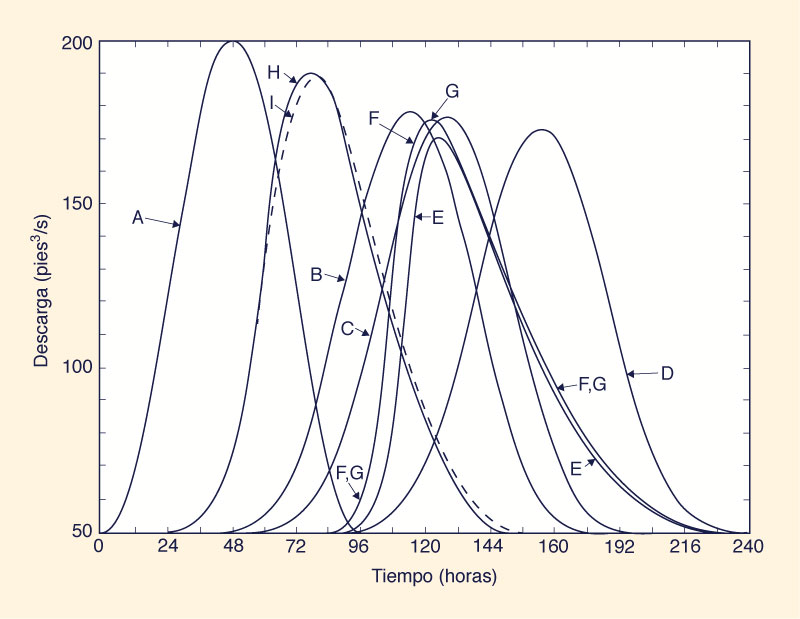
en la cual t está dado en horas.

Thomas aplicó un método aproximado para el enrutamiento la onda de inundación a través de un canal de 200 millas (322 km) de largo, utilizando un intervalo de tiempo Δt = 12 h. El método aproximado de Thomas ignora los términos de inercia; por lo tanto, sus resultados son directamente comparables a los del método de Muskingum (tanto el método de Thomas como el de Muskingum pueden considerarse análogos numéricos de la ecuación de la onda difusiva).

La Figura 2 y la Tabla 1 resumen los resultados de los cálculos utilizando el método Muskingum-Cunge con parámetros variables. Para fines de comparación, también se muestran los cálculos que utilizan parámetros constantes para tres valores de referencia de descarga.

Fig. 2   Hidrogramas descritos en la Tabla 1.

La evaluación de la Fig. 2 permite concluir lo siguiente:

1. El método Muskingum-Cunge con parámetros constantes (hidrogramas B, C y D) muestra resultados que dependen del valor de caudal de referencia elegido para evaluar los parámetros constantes. Cuanto mayor sea la descarga de referencia, más rápida será la velocidad de desplazamiento y menor la atenuación de la onda de inundación (3). Los hidrogramas de flujo de salida calculados muestran una deformación insignificante de la forma inicialmente sinusoidal, lo que implica que la suposición del parámetro constante equivale a una suposición de linealidad.

2. El método Muskingum-Cunge con parámetros variables (hidrogramas E, F y G) muestra resultados que caen dentro del rango considerado por los cálculos de parámetros constantes. La notable pendiente del brazo ascendente en los hidrogramas de salida calculados indica que se está teniendo en cuenta la no linealidad del fenómeno. Los métodos de tres y cuatro puntos dan resultados similares; sin embargo, el método de dos puntos muestra un pico más pequeño y una velocidad de desplazamiento algo más lenta. Además, el método de dos puntos da como resultado alguna pérdida de masa, como se indica en la columna 8 de la Tabla 1.

3. Los resultados de los métodos de parámetros variables de Thomas y de cuatro puntos son comparables (hidrogramas I y H). El hidrograma de parámetro variable de tres puntos (no mostrado) también está muy cerca de los resultados de Thomas.

5.  RESUMEN Y CONCLUSIONES

Se investiga el método Muskingum-Cunge en el cual se permite que los parámetros K y X varíen en el tiempo y el espacio. Se demuestra que un enfoque de tres puntos y un enfoque iterativo de cuatro puntos para el cálculo de los parámetros variables son lo suficientemente precisos en la simulación de caudales de inundación. Se muestra que un enfoque de dos puntos es inexacto en el cálculo de la descarga máxima y el tiempo de traslación de la onda. Además, el método de dos puntos da como resultado una pérdida considerable de masa.

APéNDICE - BIBLIOGRAFíA