The convergence of implicit bed transient models Victor M. Ponce, M. ASCE, Horst Indlekofer, and Darly B. Simons, F. ASCE Online version 2019 [Original version 1979]

1.  INTRODUCTION

The essential feature of a numerical model is the replacement of a derivative such as ∂ƒ/∂s by a ratio of finite differences such as Δƒ/Δs. In doing so, the numerical model must satisfy certain requirements of stability and convergence. Stability refers to the ability of the numerical scheme to inhibit the generation of error growth. Convergence is a measure of the smallness of the discretization error.

In practice, stability is a necessary condition for model operation since an unstable model is of little or no use. In numerical models, stability is usually achieved at the expense of convergence. Therefore, convergence is the focal issue: Once the model is shown to be stable, it then becomes necessary to assess its convergence properties.

The von Neumann method (5) for the systematic analysis of stability and convergence has been recognized in the literature (8) as a powerful analytical tool to study the properties of numerical models. The method will be applied herein to study the convegence properties of implicit numerical models of bed transient propagation in subcritical alluvial channel flow. Cunge and Perdreau (2), Mahmood and Ponce (4), and Ponce, et al. (7) have developed numerical models of bed transient propagation. Cunge and Perdreau studied the numerical properties of their model but fell short of generalizing their findings with respect to channel friction and sediment transport. The analysis presented herein shows that it is possible to isolate the relevant friction and transport parameters, thus providing an increased understanding of the convergence properties of implicit bed transient models.

2.  GOVERNING EQUATIONS

The governing equations of one-dimensional alluvial channel flow are: (1) The water continuity; (2) the sediment continuity; and (3) the equation of motion. Expressed per unit of channel width, they are of the following form:

Water continuity equation:

∂q           ∂d            _____  +  _____  =  0   ∂x           ∂t

(1)

Sediment continuity equation:

∂gs         ∂                                       ∂z ____  +  ____ (Cs d)  +  (1 - p) ρs g ____  =  0  ∂x          ∂t                                       ∂t

(2)

Equation of motion:

1       ∂u           u       ∂u            ∂h             τb ____  _____  +   ____  _____  +   _____  +   _______  =  0   g       ∂t            g       ∂x            ∂x           ρw gd

(3)

in which u = mean velocity; h = water surface elevation; z = channel bed elevation; d = flow depth = h - z; q = unit-width water discharge = ud; g_s = unit-width bed material transport rate; p = porosity of the material deposited in the channel bed; g = acceleration of gravity; ρ_w = density of water; ρ_s = density of solids; τ_b = bottom shear stress; x = space variable, and t = time variable.

Two supplementary equations describing the bottom friction and bed material transport are necessary. The bottom friction can be expressed by a Chézy-type relationship of the following form:

τb = ƒρw u 2

(4)

in which ƒ is a dimensionless friction factor defined as follows:

g ƒ =  _____          C 2

(5)

and C = Chézy coefficient. For steady uniform flow, the bottom shear stress is:

τbo = ƒρw uo2

(6)

Likewise:

τbo = ρw g do So

(7)

in which S_o = bottom slope. Therefore, from Eqs. 6 and 7:

So = ƒFo2

(8)

in which F_o is the steady uniform flow Froude number, defined as follows:

uo Fo =  __________            (g do) 1/2

(9)

The bed material transport rate is modeled by a Colby-type (1) relationship of the following form:

gs = k um

(10)

in which k and m are empirical bed material transport parameters.

3.  SIMPLIFIED EQUATIONS

In flow well in the subcritical range (F_o ≤ 0.6), the alluvial bed transients travel downstream with a celerity that is several orders of magnitude smaller than that of the water surface transients. This time scale difference enables the solution for the bed transients assuming a known water discharge within one time step, thereby reducing the problem to two equaitons (sediment continuity and motion) in two unknowns (water surface level and channel bed level). Furthermore, for F_o ≤ 0.6, the spatial concentration term in Eq. 2 is small compared to the remaining terms (4); therefore, it is neglected here. To facilitate the analysis, and partly on the basis of an order of magnitude reasoning, the local acceleration term in Eq. 3 is also neglected here.

Substituting Eq. 10 into Eq. 2, and expressing u in terms of q and d

∂                                           ∂z k qm _____ ( d -m ) +  ( 1 - p ) ρs g _____  =  0           ∂x                                           ∂t

(11)

Operating on Eq. 11:

m k qm        ∂d                                ∂z ( - _________ ) ______  +  ( 1 - p ) ρs g _____  =  0        d m+1          ∂x                                 ∂t

(12)

Substituting Eq. 10 into Eq. 12

m gs         ∂d                                ∂z ( - _______ ) ______  +  ( 1 - p ) ρs g _____  =  0          d            ∂x                                 ∂t

(13)

Dividing by u ( 1 - p ) ρ_s g

m cb                ∂d               1          ∂z [ - ______________ ] ______  +  ( _____ ) ______  =  0                     ρs            ∂x               u          ∂t       ( 1 - p ) ____                     ρw

(14)

in which c_b = bed material concentration in parts per unity, defined as

gs cb  =  ___________             ρw g u d

(15)

In Eq. 14, expressing u in terms of q and d, and d in terms of h and z

m cb                ∂h                    m cb                ∂z             h - z          ∂z [ - ______________ ] ______  +  [ ______________ ] ______  + ( _______ ) ______ =  0                     ρs            ∂x                             ρs          ∂x                q            ∂t       ( 1 - p ) ____                             ( 1 - p ) ____                     ρw                                            ρw

(16)

Substituting Eq. 4 into Eq. 3

u      ∂u        ∂h         ƒu2 ____ _____ + _____ + _____ =  0   g      ∂x        ∂x         gd

(17)

In Eq. 18, expressing u in terms of q and d, and d in terms of h and z

q 2        ∂h             q 2        ∂z         ƒq 2 ( 1 - ______ ) _____ + ( ______ ) _____ + ______ =  0          g d 3       ∂x           g d 3       ∂x        g d 3

(18)

4.  LINEAR STABILITY ANALYSIS

Equations 16 and 18 must satisfy both the equilibrium flow for which h = h_o, z = z_o, c_b = c_bo, and d = d_o, and the transient flow, for which h = h_o + h^', z = z_o + z^', c_b = c_bo + c^'_b, and d = d_o + d^'. The superscript ^' represents a small perturbation to the equilibrium flow. Thus, all quadratic terms in the perturbed components may be neglected due to an order of magnitude reasoning.

Substitution of the perturbed variables in Eq. 16 yields the following equaiton:

∂h'              ∂z'          ho - zo        ∂z' -Ao _____ + Ao ______ + __________ ______ =  0         ∂x               ∂x              q             ∂t

(19)

in which:

m cbo Ao  = _______________                          ρs             (1 - p) ______                          ρw

(20)

From Eqs. 9, 10 and 15:

k Fo 2 uo m - 3 cbo  =  ________________                       ρw

(21)

Therefore:

Ao = φ Fo 2

(22)

in which φ is a composite bed material transport parameter defined as follows:

m k uo m - 3 φ = ______________            (1 - p) ρs

(23)

Substituting Eq. 22 into Eq. 19:

∂h'                    ∂z'         ho - zo      ∂z' -φ Fo2 _____  + φ Fo2 _____  + _________ _____  = 0              ∂x                     ∂x             q           ∂t

(24)

Substitution of the perturbed variables in Eq. 18 yields the following equaiton:

∂h'                ∂z'                      h' - z'       (1 - Fo 2) _____  + Fo2 _____ - 3ƒFo2 ( _________ ) = 0                  ∂x                ∂x                      ho - zo

(25)

in which:

q 2 Fo 2  =  _______               g do3

(26)

5.  ANALYTICAL SOLUTION

The solution of the system of Eqs. 24 and 25 is postulated in the following exponential form:

h' ____ = h* exp [i (σ* x* - β* t*)]   do

(27)

and

z' ____ = z* exp [i (σ* x* - β t*)]   do

(28)

in which:

2π σ* = ( _____ ) Lo              L

(29)

2π        Lo β*R =  ( _____ ) _____                 T         uo

(30)

β*I = attenuation (or amplification) factor

(31)

x x* = ____          Lo

(32)

uo t* = t _____            Lo

(33)

and

do Lo = _____           So

(34)

in which L = wavelength; T = wave period; and h_* and z_* are dimensionless amplitude functions.

The dimensionless celerity, c_*, of a sinusoidal disturbance is defined as follows (6):

L         ___          T         β*R c* = ____ = ______          uo         σ*

(35)

The logarithmic decrement, δ(6), is defined as follows:

β*I δ = 2π ________              | β*R |

(36)

The substitution of Eqs. 27 and 28 into Eqs. 24 and 25 results in a homegeneous system of linear equations in the unknowns h_* and z_*. The nontrivial condition for the determinant of the coefficient matrix leads to a transport-normalized dimensionless celerity, c_*aφ, expressed as follows:

c*a            Fo2(1 - Fo2)σ*2 c*aφ = _____ = ____________________               φ            (1 - Fo2)σ*2 + 9

(37)

and a logarithmic decrement, δ_a, expressed as follows:

6π δa = - ____________             |1 - Fo2|σ*

(38)

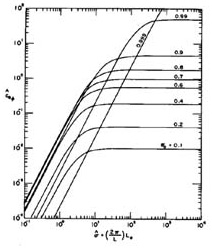
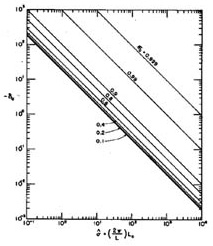
Figures 1 and 2 show the transport-normalized dimensionless celerity, c_*aφ, and logarithmic decrement, δ_a, as a funtion of the equilibrium flow Froude number, F_o, and the dimensionless wave number, σ_*, in subcritical flow.

Fig. 1  Transport-normalized dimensionless analytical celerity c*aφ versus dimensionless wave number σ* in subcritical flow.

Fig. 2  Logarithmic decrement of analytical solution δa versus dimensionless wave number σ* in subcritical flow.

---

6.  NUMERICAL SOLUTION

The four-point implicit scheme of Preissmann (3) is used to discretize the governing equations. The finite difference equations are of the following form (Fig. 3):

Fig. 3  Definition sketch for four-point implicit scheme.

θ                                  1 - θ ƒ(x,t) = ___ (ƒj + 1n + 1 + ƒjn + 1) + ______ (ƒj + 1n + ƒjn)               2                                     2

(39)

∂                   1 ____ ƒ(x,t) ≈ _____ (ƒj + 1n + 1 - ƒj + 1n + ƒjn + 1 - ƒjn)  ∂t                  2∆t

(40)

∂                   θ                               1 - θ ____ ƒ(x,t) ≈ _____ (ƒj + 1n - ƒjn + 1) + ______ (ƒj + 1n - ƒjn)  ∂x                 ∆x                                ∆x

(41)

in which ƒ(x,t) = a dependent variable; Δx = space interval; Δt = time interval; and θ = weighting factor of the scheme.

Let us call η = h^' and ζ = z^', and Eqs. 24 and 25 convert to:

∂η                  ∂ζ        do      ∂ζ -φ Fo2 _____ + φ Fo2 ____ + _____ _____ = 0              ∂x                  ∂x         q       ∂t

(42)

∂η               ∂ζ                   η - ζ     (1 - Fo2) _____ + Fo2 ____ - 3ƒFo2 (_______) = 0                 ∂x               ∂x                     do

(43)

Substituting Eqs. 39-41 into 42 and 43 yields:

θ                               1 - θ                                      θ -φFo2[_____ (ηj+1n+1 - ηjn+1) + ______ (ηj+1n - ηjn)] + φFo2[_____ (ζj+1n+1 - ζjn+1)              Δx                                Δx                                      Δx      1 - θ                            do + _______ (ζj+1n - ζjn)] + _______ [ζj+1n+1 - ζj+1n + ζjn+1 - ζjn] = 0        Δx                           2qΔt

(44)

θ                               1 - θ                                   θ (1 - Fo2)[_____ (ηj+1n+1 - ηjn+1) + ______ (ηj+1n - ηjn)] + Fo2[_____ (ζj+1n+1 - ζjn+1)                  Δx                                Δx                                   Δx      1 - θ                       -3ƒFo2       θ + _______ (ζj+1n - ζjn)] _______ {[ ____ (ηj+1n+1 + ηjn+1)        Δx                          do            2      1 - θ                               θ                                1 - θ + _______ (ηj+1n + ηjn)] - [ _____ (ζj+1n+1 + ζjn+1) + _______ (ζj+1n + ζjn) ]} = 0         2                                  2                                   2

(45)

The substitution of Eqs. 27 and 28 into Eqs. 44 and 45 yields:

Δt*                                                   Δt*                     E h*[ -φFo2 (θE + 1)( _____ ) i tanα]+ z*[ φFo2 (θE + 1)( _____ ) i tanα + ____ ] = 0                                   Δx*                                                  Δx*                     2

(46)

Δt*                   3 h*[ (1 - Fo2) (θE + 1)( _____ )i tanα - ____(θE + 1)Δt*]                                       Δx*                  2                                  Δt*                     3 + z*[ Fo2 (θE + 1)( _____ ) i tanα + ____(θE + 1)Δt*] = 0                                  Δx*                    2

(47)

in which:

E = e -iβ*Δt* - 1

(48)

Δx Δx* = _____             Lo

(49)

uo Δt* = Δt _____                 Lo

(50)

and

σ*Δx* α = ________             2

(51)

Equations 46 and 47 constitute a homogeneous system of linear equations in the unknowns h_* and z_*. For the solution to be nontrivial, the determinant of the coefficient matrix must vanish. This leads to:

1        c*a                                        3        c*a E [ φθσ*Fo2 tan2α - ____ ( _____ ) σ* (1 - Fo2) i tanα + ____ ( _____ ) α ]                                    2         C                                         2         C + φσ*Fo2 tan2α = 0

(52)

in which C is the bed transient Courant number defined as follows:

L          ___           T               Δt C = ______ = ca _____          Δx              Δx         ____          Δt

(53)

Since:

c*a c*aφ = _____               φ

(54)

Equation 52 reduces to:

1       c*aφ                                       3      c*aφ E [ φσ*Fo2 tan2α - ___ ( ______ ) σ* (1 - Fo2) i tanα + ___ ( ______ ) α ] + σ*Fo2 tan2α = 0                                 2         C                                         2        C

(55)

Solving Eq. 55 for E:

M + i N exp (-iβ*Δt*)  =  1 - ________                                     P

(56)

in which:

3       c*aφ M = θ (σ*Fo2 tan2α)2 + ___ ( ______ ) (σ*Fo2 α tan2α)                                        2        C

(57)

1       c*aφ N = ___ ( ______ ) σ*2 (1 - Fo2)Fo2 tan3α         2         C

(58)

3       c*aφ                  1       c*aφ P = [ θσ*Fo2 tan2α + ___ ( ______ )α ]2 + [ ___ ( ______ )σ* (1 - Fo2) tanα]2                                     2         C                     2         C

(59)

In Eq. 56, expressing β_* into its real and imaginary components

β* = β*R + i β*I

(60)

it follows that:

N tan (β*R Δt*) = _______                          P - M

(61)

and

[(P - M) 2 + N 2]1/2 exp(β*I Δt*) = ___________________                                     P

(62)

The dimensionless celerity of the numerical solution, c_*n, is defined as follows:

N                              tan-1( ________ )             β*R                        P - M c*n = ________ = ___________________               σ*                    σ* Δt*

(63)

Since

2α σ* Δt* = ______                 c*a                _____                  C

(64)

and defining

c*n c*nφ = _____               φ

(65)

Equation 63 reduces to the following:

c*aφ                     N             ( ______ ) tan-1 ( _______ )                   C                    P - M c*nφ = ___________________________                             2α

(66)

The logarithmic decrement of the numerical solution, δ_n, is defined as follows:

[(P - M)2 + N 2]1/2                 β*I               ln { ____________________ }                                                         P δn = 2π _______ = 2π _____________________________               |β*R |                                    N                                          |tan-1 ( _______ )|                                                        P - M

(67)

Equations 66 and 67 enable the calculation of the propagation celerity, c_*nφ, and logarithmic decrement, δ_n, of the four-point implicit numerical analog of Eqs. 2 and 3, as a function of: (1) The Froude number of the equilibrium flow, F_o = u_o / (gd_o)^1/2; (2) the dimensionless wave number, σ_*, of the transient component of the motion, σ_* = (2π / L)L_o; (3) the spatial resolution parameter, α = π / (L / Δx); (4) the bed transient Courant number, C = c_a Δt / Δx; and (5) the weighting factor of the scheme, θ.

---

7.  CONVERGENCE ANALYSIS

The convergence analysis is based on the following ratios:

R1 = exp (δn - δa)

(68)

c*nφ R2 = _______           c*aφ

(69)

The value R₁ is the attenuation ratio and R₂ is the translation ratio. For (δ_n - δ_a) > 0, R₁ > 1, leading to numerical amplification; for (δ_n - δ_a) < 0, R₁ < 1, leading to numerical attenuation. For R₂ > 1, the numerical translation is greater than the physical translation; for R₂ < 1, the numerical translation is smaller than the physical translation. For R₁ = R₂ = 1, there is an exact coincidence between analytical and numerical solutions.

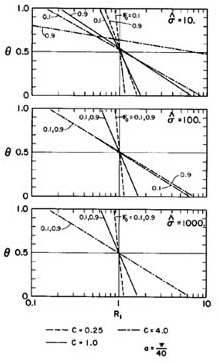
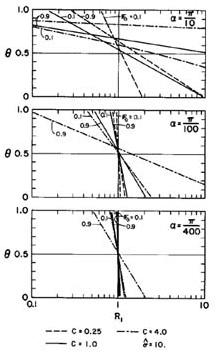
Figures 4 and 5 show the attenuation ratio, R₁, as a function of F_o, σ_*, α, C and θ. In Fig. 4, α is kept constant and equal to π / 40; in Fig. 5, σ_* is kept constant and equal to 10. Figures 4 and 5 show that increasing σ_* and decreasing F_o, α and C result in improved convergence of the wave amplitude, i.e., R₁ → 1.0. A value of θ = 0.5 is a necessary condition for stability (R₁ < 1), but it is not sufficient for the general case. Instability (R₁ > 1) may be observed for certain combinations of F_o, σ_*, and α, even though θ > 0.5. Interestingly enough, this behavior has been observed in actual model operation (2,4,7).

Fig. 4  Attenuation raio R1 as function of Fo, σ*, C, and θ; α = π/40.

Fig. 5  Attenuation raio R1 as function of Fo, α, C, and θ; σ* = 10.

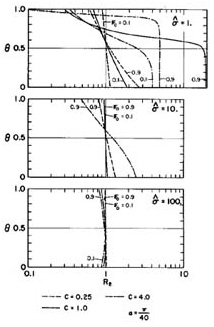
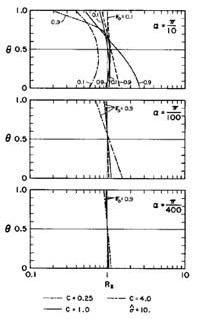
Figures 6 and 7 show the translation ratio, R₂, as a funtion of F_o, σ_*, α, C and θ. In Fig. 6, α is kept constant and equal to π / 40; in Fig. 7, σ_* is kept constant and equal to 10. Again, Figs. 6 and 7 show that increasing σ_* and decreasing F_o, α, and C result in improved convergence of the wave translation, i.e., R₂ → 1.0.

Fig. 6  Translation raio R2 as function of Fo, σ*, C, and θ; α = π/40.

Fig. 7  Translation raio R2 as function of Fo, α, C, and θ; σ* = 10.

The results of Figs. 4-7 enable the following conclusions to be drawn: (1) Convergence improves for a sufficiently high value of σ_*, and for low values of F_o, α, and C; and (2) a value of θ midrange between 0.5 and 1.0 will in general satisfy both stability and convergence requirements. Based on the analysis made, the following range of parameters are recommended: σ_* ≥ 10; F_o ≤ 0.6; α ≤ π / 40; C ≤ 2; and 0.6 ≤ θ ≤ 0.8.

In practice, σ and F_o are determined by the characteristics of the problem at hand. The recommended values for α, C, and θ are to be taken only as guidelines. Numerical experimentation is necessary in order to assess the sensitivity of the results of the model to the convergence parameters. The numerical experiments are aimed at achieving a satisfactory convergence (i.e., minimizing numerical dispersion) while maintaining stability.

---

8.  SUMMARY AND CONCLUSIONS

A comprehensive theoretical treatment of the convergence of the four-point implicit numerical model of alluvial channel bed transients is presented. The dimensionless celerity and logarithmic decrement of the analytical and numerical solutions are calculated. Convergence is tested by establishing the ratio of celerities (translation convergence) and the ratio of attenuation factors (attenuation convergence). Two physical and three numerical parameters are identified: the equilibrium flow Froude number, the transient flow dimensionless wave number, the spatial resolution, the Courant number, and the weighting factor of the scheme.

---

ACKNOWLEDGMENTS

The research presented in this paper was supported in part by the Colorado State University Experimental Station. H. Indlekofer's visit to Colorado State University was made possible by a NATO fellowship.

---

APPENDIX Ι. REFERENCES

1. Colby, B, R., "Discharge of Sands and Mean Velocity Relationships in Sand-Bed Streams," Professinal Paper 462-A, United States Geological Survey, Washington, D.C., 1964.

2. Cunge, J. A., and N. Perdreau. 1973. "Mobile Bed Fluvial Mathematical Models," La Houille Balanche, Grenoble, France, No. 7, 561-580.

3. Liggett, J. A., and J. A. Cunge. 1975. "Numerica Methods of Solution of the Unsteady Flow Equations," Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Fort Collins, Colo., 89-182.

4. Mahmood, K., and V. M. Ponce. 1976. "Mathematical Modeling of Sedimentation Transients in Sand-Bed Channels," Report CER75-76-KM-VMP28, Engineering Research Center, Colorado State University, Fort Collins, Colo., Apr.

5. O'Brien, G. G., M. A. Hyman, and S. Kaplan. 1951. "A study of the Numerical Solution of Partial Differential Equations," Journal of Mathematics and Physics, Vol. 29, No. 4, 223-251.

6. Ponce, V. M., and D. B. Simons. 1977. "Shallow Wave Propagation in Open Channel Flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12. Proc. Paper 13392, Dec., 1461-1476.

7. Ponce, V. M., J. Lopez Garcia, and D. B. Simons. 1979. "Modeling Alluvial Channel Bed Transients," Journal of the Hydraulics Division, ASCE, Vol. 105, No. HY3. Proc. Paper 14456, Mar., 245-256.

8. Roache, P. J. 1972. Computational Fluid Dynamics, Hermosa Publishers, Albuquerque, NM.

---

APPENDIX ΙΙ. NOTATION

The following symbols are used in this paper:

A_o = parameter, Eq. 20;

C = Chézy coefficient and bed transient Courant number;

c_a = analytical celerity;

c_b = bed material concentration, Eq. 15;

c_n = numerical celerity;

c_* = dimensionless celerity, Eq. 35;

c_*a = dimensionless analytical celerity;

c_*n = dimensionless numerical celerity;

c_*aφ = transport-normalized dimensionless analytical celerity, Eq. 37;

c_*nφ = transport-normalized dimensionless numerical celerity, Eq. 66;

d = flow depth;

E = parameter, Eq. 48;

F = Froude number;

ƒ = dimensionless friction factor, Eq. 5, and dependent variable;

g = acceleration of gravity;

g_s = unit-width bed material transport rate;

h = water surface elevation;

j = space discretization index;

k = empirical bed material transport parameter, Eq. 10;

L = wavelength;

L_o = reference channel length, Eq. 34;

M = parameter, Eq. 57;

m = empirical bed material transport parameter, Eq. 10;

N = parameter, Eq. 58;;

n = time discretization index;

P = parameter, Eq. 59;

p = porosity of bed material;

q = unit-width water discharge;

R₁ = attenuation ratio, Eq. 68;

R₂ = translation ratio, Eq. 69;

S_o = bottom slope;

T = wave period;

t = time variable;

u = mean velocity;

x = space variable;

z = bed elevation

α = spatial resolution parameter, Eq. 51;

β_*I = attenuation (or amplification) factor;

β_*R = dimensionless frequency, Eq. 30;

Δt = time interval;

Δx = space interval;

δ = logarithmic decrement, Eq. 36;

δ_a = logarithmic decrement of analytical solution, Eq. 38;

δ_n = logarithmic decrement of numerical solution, Eq. 67;

ζ = bed elevation perturbation;

η = water surface elevation perturbation;

θ = weighting factor of implicit scheme;

ρ_s = density of solids;

ρ_w = density of water;

σ_* = dimensionless wave number, Eq. 29;

τ_b = bottom shear stress; and

φ = composite bed material transport parameter, Eq. 23.

Subscripts

o = equilibrium flow.

Superscripts

* = dimensionless variable;

' = perturbed variable.

---