1. MUSKINGUM VS MUSKINGUM-CUNGE METHODS
The Muskingum-Cunge method is a method of flood routing that improves on the classical Muskingum method
(Chow, 1959) by using physical-numerical principles established by Cunge to calculate the routing parameters
(Cunge, 1969). By way of comparison, it may be affirmed that while the classical Muskingum method is hydrologic in nature,
the Muskingum-Cunge method has a distinct hydraulic basis.
Table 1 compares both methods, describing their differences.
McCarthy, G. T. 1938. "The unit hydrograph and flood routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, June 24. Cunge. J. A. 1969. "On the subject of a flood propagation
computation method (Muskingum Method)," Journal of Hydraulic Research, Vol. 7, No. 2, 205-230. Chow, V. T. 1959. Open-channel Hydraulics, Mc-Graw Hill, New York, Ponce, V. M. 2014. "The Muskingum-Cunge method,"
Section 10.6 of
Fundamentals of Open-channel Hydraulics, online textbook. Hydrologic method, where the routing parameters
K and X are calculated by trial-and-error calibration,
using a pair of inflow-outflow hydrographs measured in a gaged river
reach.
Hydraulic method, where the routing parameters K and X are based on the channel morphology, as represented by the
prevailing channel slope and
cross-sectional-shape characteristics. The availability of measured flood hydrographs suited for parameter calibration.
The availability of geometric and hydraulic channel data,
to the extent that this data properly represents the
reach under consideration.
Good with any computational tool, including a spreadsheet, programming, and available commercial and government software.
Good with any computational tool, including a spreadsheet, programming, and available commercial and government software.
Good for the reach and event
used for calibration;
poor for any other reach or flood event.
Very good for all events within the reach under consideration; only
limited to the extent that the geometric and hydraulic channel data
must be representative of the reach. Very limited; usually not available due to large hydrologic data requirements.
Available at the cost of additional complexity. Dated method; limited in
accuracy when used for extensive watershed/basin routing.
Newer method, featuring state-of-the-art hydraulic numerical modeling knowledge; ideally
suited for extensive watershed/basin routing.
Given the facts described in Table 1,
we posit that the Muskingum-Cunge method is altogether theoretically better
than the Muskingum method. Thus, we encourage its wider
use in U.S. and world
hydrologic and hydraulic engineering modeling practice.
2. MUSKINGUM-CUNGE AND FLOOD WAVES
The key to the understanding of the theoretical basis of the Muskingum-Cunge method is the
recognition that the diffusion wave applies through a wider range than competing waves such
as the kinematic and dynamic waves (Ponce and Simons,
1977). Kinematic waves do not attenuate, while most flood waves
attenuate at least a little bit; on the other hand, dynamic waves attenuate too much and, therefore,
do not represent flood
waves in typical cases. A diffusion wave,
lying in the midrange of attenuation, is, by far,
the most applicable wave model from the standpoint of practice.
This fact was recognized early by McCarthy in 1938 (Fig. 1)
and later by Cunge in 1969. However, unlike McCarthy,
Cunge tied the Muskingum method to the properties of the governing
diffusion wave.
Fig. 1 The Muskingum river near Marietta, Ohio. Given the demonstrated simplicity of the Muskingum-Cunge method, particularly when compared to alternative hydraulic routing models, the former remains a strong candidate among the gamut of available routing models. This is particularly the case in view of the fact that hydraulic routing methods are generally unsuited for hydrologic applications involving intensive watershed/basin routing, where, clearly, the use of a much simpler method is advised. Thus, the Muskingum-Cunge method emerges as the only diffusion-wave routing model which is simple and accurate enough to be suited for large-scale hydrologic modeling applications. In the remainder of this paper, we andeavor to make the case for justifying this assertion.
3. MUSKINGUM-CUNGE AND COMPUTATIONAL ACCURACY
The strength of the Muskingum-Cunge method is clearly its theoretical basis as an analog of the
diffusion wave equation. Cunge realized that the Muskingum method and the kinematic wave model
shared the same theoretical basis. Furthermore, Cunge was able to calculate the error of the
first-order numerical scheme (i.e., the Muskingum method)
and to tie this error to the hydraulic diffusivity
of the diffusion wave (Hayami, 1951). This accomplishment paved the way for the calculation of
routing parameters in terms of geometric and hydraulic variables, thus
circumventing the need for
the expensive and impractical streamgage measurements.
The Muskingum-Cunge method is accurate because of its strong theoretical basis.
Its numerical properties, including stability and convergence, have been extensively documented
both in theory and in practice (Ponce and Vuppalapati, 2016). The method is strongly stable
and with excellent convergence properties for values of Courant number in the neighborhood of
1. This property
of strong stability and excellent convergence all but assures its grid independence,
i.e., the property of a numerical scheme to reproduce the same result, regardless
of grid resolution. Competing (numerical) methods, including the kinematic wave, can be shown to lack grid independence,
casting a cloud on their theoretical correctness (Ponce, 1986).
In summary, the Muskingum-Cunge method is the only numerical analog of the diffusion wave equation
based on a straight-forward, explicit, point-by-point computation, all-the-while
featuring grid independence. No other flood routing
method can claim this particular set of properties at this time.
4. ROUTING EQUATIONS
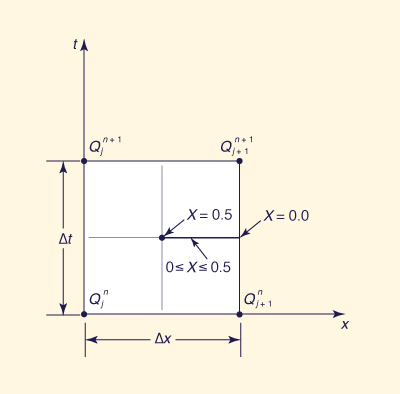
The basic routing equation of the Muskingum-Cunge method is the following (Fig. 2):
Fig. 2 Definition sketch.
in which j is a spatial index, n is a temporal index and C0, C1 and C2 are calculated as follows:
The parameters K and X are calculated as follows (Cunge, 1969; Ponce, 2014):
in which Δx = reach length (space interval); c = flood wave celerity; q =
unit width discharge; and
5. LINEAR VS NONLINEAR ROUTING
In Nature, flood waves exhibit a nonlinear behavior, i.e., their celerity and attenuation properties (tend to) vary with the flow.
The magnitude of this effect varies with the cross-sectional shape in predictable ways.
Three asymptotic cross-sectional shapes are recognized (Ponce, 2014):
Hydraulically wide,
Triangular, and
Inherently stable.
The inherently stable channel is that for which the hydraulic radius is a constant in the overflow channel.
The shape of the inherently stable channel has been calculated by
Ponce and Porras (1995) (Fig. 3).
Fig. 3 The inherently stable cross-sectional shape. It can be shown that the nonlinear effect is strongest for hydraulically wide channels, weak for triangular channels, and totally nonexistent for inherently stable channels. In practice, most cross-sectional shapes are likely to be close to being hydraulically wide. Thus, the nonlinear effect may be marked in certain, if not typical, cases. Notwithstanding the nonlinear effect, there are two ways to calculate the routing parameters in Muskingum-Cunge routing (Ponce and Yevjevich, 1978):
In the linear approach, the routing parameters K and X are based on average (or representative) hydraulic variables (c and q) and kept constant throughout the computation. In the nonlinear approach, the routing parameters are allowed to vary with the flow, i.e., to vary for each computational cell as a function of local flow variables. The tradeoffs between linear and nonlinear Muskingum-Cunge routing are described in Table 2.
6. DISCUSSION
The Muskingum-Cunge method represents a considerable improvement in
computational accuracy when compared with
the related Muskingum method. The only caveat is that the parameter calculation (Eqs. 5 and 6) should be based on values of
flood wave celerity c and unit-width discharge q that are representative of the reach under consideration. To acomplish this objective, it is recommended that GIS-supported
geometric and hydraulic data
be used to better estimate the relevant
input data and variables on which to base the calculation of the
routing parameters.
7. SUMMARY
The Muskingum-Cunge method is reviewed to further clarify its theoretical basis and encourage
its wider acceptance and use in current hydrologic engineering practice.
Its theoretical background
and computational accuracy are reviewed and clarified.
The method is recognized to be
the only numerical analog of the diffusion wave equation
based on a straight-forward, explicit, point-by-point computation, all-the-while
featuring grid independence. We note that no other flood routing
method can claim this particular set of properties at this time.
REFERENCES
Chow, V. T. 1959. Open-channel Hydraulics. Mc-Graw Hill, New York.
Cunge, J. A. 1969. On the
Subject of a Flood Propagation Computation Method (Muskingum Method), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, December.
McCarthy, G. T. 1938. The Unit Hydrograph and Flood Routing.
Unpublished manuscript, presented at a Conference of the
North Atlantic Division, U.S. Army Corps of Engineers, June 24.
Natural Environment Research Council. 1975.
Flood Studies Report. Vol. 3: Flood Routing. London. England.
Ponce, V, M., and D. B. Simons. 1977. Shallow
wave propagation in open-channel flow.
Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, 1461-1476.
Ponce, V. M., and V. Yevjevich. 1978.
Muskingum-Cunge method with variable parameters.
Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, December, 1663-1667.
Ponce, V. M. 1986. Diffusion Wave Modeling of Catchment Dynamics.
Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, August, 716-727.
Ponce, V. M., and P. J. Porras. 1995. Effect of cross-sectional shape on free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, April,
376-380.
Ponce, V. M. 2014. Fundamentals of open-channel hydraulics. Online textbook.
Ponce, V. M., and B. Vuppalapati. 2016.
Muskingum-Cunge amplitude and phase portraits with
online computation. Online article.
APPENDIX: Origin of the term Muskingum-Cunge
In a hydrologic context, the word "Muskingum" is taken from the Muskingum river,
in eastern Ohio.
The term "Cunge" gives the proper credit to Jean A. Cunge, a Polish-French engineer
who, in 1969, published the equations used in the Muskingum-Cunge method.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||