|
DRENAJE DE CARRETERAS - B
[C]
[A]
Victor Miguel Ponce
Septiembre 2017
4. ALCANTARILLAS
4.1 Tipos de alcantarillas
Las alcantarillas son conductos de drenaje de longitud corta,
ubicados en las intersecciones de la red natural de
drenaje (quebradas, arroyos, ríos) con las redes de transporte (carreteras, caminos,
vías de ferrocarril, etc.).
Las alcantarillas son mucho más pequeñas que los puentes; por consiguiente,
hay un mayor número de ellas. Usualmente están
diseñadas para operar bajo
flujo permanente gradualmente variado; por lo tanto se aplican
los principios de la Sección 3.
Las alcantarillas se calculan
para que permitan pasar de manera óptima el gasto
de diseño, sin producir un desbordamiento tal que comprometa la integridad de la
superestructura (Fig. 66). El gasto
de diseño está basado en consideraciones
hidrológicas,
las cuales están tratadas en la
Sección 2.
El período de retorno varía típicamente
entre 10 y 50 años (Ponce, 2008).
A mayor período de retorno, mayor será el gasto de
diseño y, consecuentemente, mayores serán
las dimensiones de la estructura.
|
Fig. 66 Alcantarilla del Cañón Yogurt, en la frontera
internacional
entre California, EE.UU. y Baja California, México.
|
El flujo en una alcantarilla depende de lo siguiente:
-
El tamaño y la forma de
la sección transversal,
-
La pendiente de fondo,
-
La longitud del conducto,
-
La rugosidad, y
-
Las características de la entrada y de la salida.
El flujo puede ser de uno de los siguientes tipos: De superficie libre (flujo en canal),
De conducto cerrado (flujo en tubería), o
De
superficie libre en una fracción
de su longitud y conducto cerrado en la otra fracción.
Las profundidades de flujo aguas arriba y
aguas abajo determinan si la
alcantarilla está fluyendo parcial o totalmente llena.
La profundidad de flujo aguas arriba,
por encima de la base o fondo en la entrada de la alcantarilla,
es denominada Profundidad Aguas Arriba [Headwater HW],
por sus siglas en Inglés.
La profundidad de flujo aguas abajo, por
encima de la base o fondo en la salida de la alcantarilla,
es denominada Profundidad Aguas Abajo [Tailwater TW].
El objetivo es calcular el tamaño más
pequeño de la alcantarilla
que permita pasar el gasto de diseño sin exceder una profundidad
aguas arriba predeterminada (Fig. 67).
El diseño depende de si el control (hidráulico)
está en la entrada o en la salida
de la alcantarilla.
|
Fig. 67 Alcantarilla debajo de la línea de ferrocarril,
Cañada Joe Bill, Tecate,
Baja California, México.
|
4.2 Control en la entrada
El flujo en una alcantarilla se encuentra bajo control en la entrada
cuando la descarga depende sólo de las condiciones
en la entrada. Por ejemplo, asúmase una alcantarilla circular de
diámetro
D, longitud L, pendiente de fondo S,
profundidad aguas arriba HW y profundidad aguas abajo TW.
El primer paso es
calcular la profundidad normal yn y la
profundidad crítica yc en el conducto (Sección 3 y calculadoras en línea).
Se examinan las siguientes condiciones:
-
Si yn <
yc, el flujo es supercrítico y
la profundidad aguas abajo no afecta a las condiciones
aguas arriba. Por lo tanto, la profundidad aguas arriba está
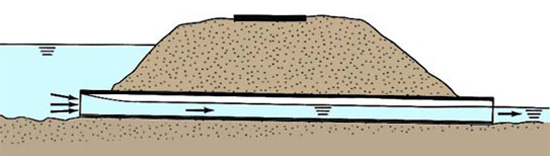
exclusivamente controlada por las condiciones en la entrada (Fig. 68).
|
Fig. 68 Flujo en una alcantarilla bajo condiciones supercríticas,
con la entrada sumergida
y la salida no sumergida.
|
|
-
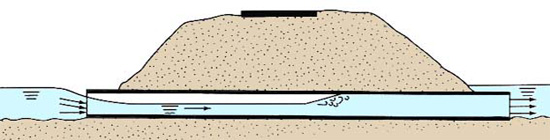
Si el flujo es supercrítico y TW > yn, puede ocurrir un salto hidráulico en algún lugar del conducto (Fig. 69).
|
Fig. 69 Flujo en una alcantarilla bajo condiciones supercríticas,
con la entrada no sumergida
y la salida sumergida.
|
|
El control en la entrada ocurre cuando la alcantarilla es capaz de
conducir más flujo que el permitido por el orificio de entrada.
La sección de control se sitúa precisamente en la entrada. El flujo pasa de profundidad
crítica en la sección de control a supercrítica aguas abajo de la misma.
Cuando el control está en la entrada, la alcantarilla actúa como
un orificio o vertedero. Si la entrada está sumergida, el flujo
es similar al de un orificio; por el contrario,
si la entrada no está
sumergida,
el flujo se asemeja al de un vertedero.
[Si HW < 1.2 D, la entrada será no sumergida].
Si la entrada no está sumergida pero la salida sí está,
se formará un salto hidráulico en algún lugar del conducto (Fig. 69).
4.3 Control en la salida
El control en la salida ocurre en las siguientes condiciones:
Cuando la profundidad
aguas abajo TW es: TW > 1.2 D; es decir,
para un nivel alto de la superficie de agua. En este caso, la alcantarilla está
completamente sumergida, lo cual se asemeja a un flujo en
conducto cerrado.
El nivel aguas arriba puede calcularse usando
la ecuación de la conservación de la energía.
El nivel aguas arriba está determinado por la elevación del nivel aguas abajo y las
características de fricción de la alcantarilla.
Cuando la entrada y la
salida se encuentran sumergidas; y
Cuando la pendiente de la alcantarilla es suave
(flujo subcrítico) y tanto el nivel aguas arriba como el nivel
aguas abajo son menores que el diámetro de la alcantarilla
(HW < D; TW < D).
En este caso, el procedimiento más apropriado es calcular el
perfil de la superficie del agua.
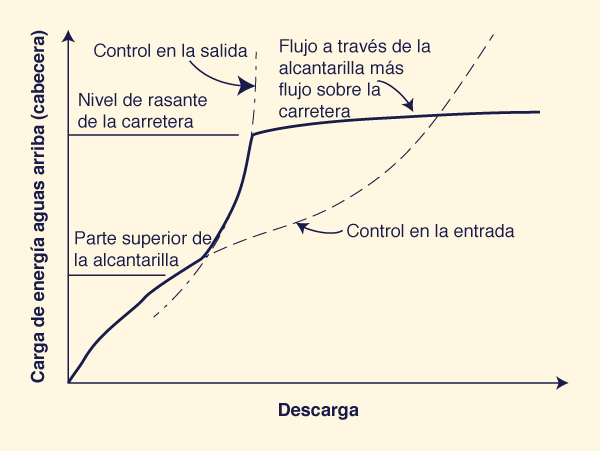
La Figura 70 ilustra la variación de la descarga o caudal en función de la carga
o nivel de energía
aguas arriba.
Puede observarse que conforme la descarga aumenta de baja a alta,
a un cierto nivel
el flujo cambia de control en la entrada a control en la salida.
|
Fig. 70 Variación de la descarga en función de la carga (nivel) de energía aguas arriba
(U.S. Army Corps of Engineers, 2014).
|
|
4.4 Diseño de alcantarillas
Pasos a seguir en el diseño de una alcantarilla:
-
Recolectar los datos de diseño:
-
Elegir el tipo y características de la alcantarilla:
-
Forma de la sección transversal (circular, cuadrada, rectangular, con arco),
-
Dimensiones (diámetro, si es circular),
-
Longitud del conducto,
-
Tipo de material (Figs. 71 y 72) (concreto, acero
corrugado, aluminio corrugado, mampostería de piedra), y
-
Tipo de entrada (con esquinas rectas o esquinas redondeadas).
|
Fig. 71 Un conjunto de dos alcantarillas de acero corrugado.
|
|
-
Determinar el tipo de control predominante
(entrada o salida), basado en: (a) la elevación
del nivel aguas arriba, (b) la elevación del nivel aguas abajo,
(c) el diámetro, y
(d) la pendiente.
-
Si el control es en la entrada, calcular la elevación
del nivel aguas arriba requerida para permitir
pasar el gasto de diseño en forma óptima.
-
Si el control es en la salida, calcular la elevación
del nivel aguas arriba requerida, usando: (a) la ecuación
de conservación de la energía, o (b) el cálculo del perfil de la
superficie del agua.
-
Si la elevación calculada del nivel aguas arriba es mayor
que la permitida, elegir una alcantarilla de mayor tamaño y repetir el proceso de cálculo.
-
En algunos casos, no es posible predeterminar
el tipo de control.
En este caso, se recomienda hacer los dos cálculos.
El tipo de control adoptado será aquél
que resulte en una mayor elevación del nivel aguas arriba.
-
Otras consideraciones en el diseño de una alcantarilla incluyen:
-
Socavación o erosión en el cuerpo del terraplén que
rodea al conducto,
-
Socavación local en la salida de la alcantarilla,
-
Erosión del material de relleno cerca de la entrada,
-
Obstrucción del conducto con escombros, y
-
Estructura para permitir el paso de peces.
|
Fig. 72 Cruce de carretera con una alcantarilla rectangular
de mampostería de piedra.
|
|
Diseño de una alcantarilla utilizando la ecuación de conservación de la energía
Diseñar una alcantarilla para las siguientes condiciones:
-
Gasto de diseño: Q = 200 pies cúbicos por segundo.
-
Período de retorno: T = 25 años.
-
Longitud del conducto: L = 200 pies.
-
Pendiente de fondo: So = 0.01.
-
Tipo de alcantarilla: Concreto.
-
n de Manning = 0.013.
-
Elevación de la base en la entrada: z1 = 100 pies.
-
Elevación de la rasante de la carretera suprayacente: Es = 110 pies.
-
Profundidad aguas abajo: TW =
y2 = 3.5 pies.
-
Bordo libre: Fb = 2 pies.
Solución
-
La elevación de diseño en el extremo aguas arriba es: Es - Fb = 100 - 2 = 108 pies.
-
Suponer una tubería de concreto circular, con esquinas rectas y
muros de cabecera.
-
Suponer que el control está en la salida.
-
Suponer que la línea de gradiente hidráulico (LGH)
está en la elevación del extremo aguas abajo.
-
Calcular la elevación en la salida: z2 = z1 -
(So L) = 100 - (0.01 × 200) = 98 pies.
-
Calcular la elevación del nivel aguas abajo: z2 + y2 = 98 + 3.5 = 101.5 pies.
-
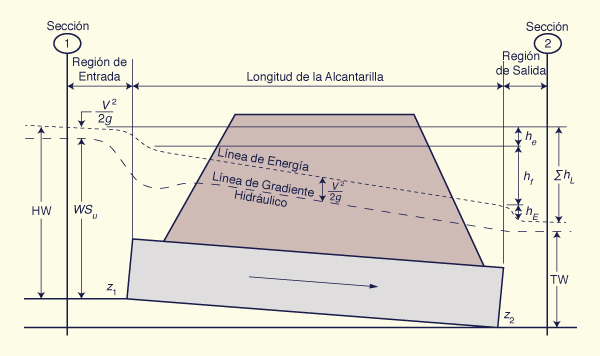
Establecer la conservación de la energía (Fig. 73):
V12 V22
z1 + y1 + _____ = z2 + y2 + _____ + ∑hL
2g 2g
| (187) |
|
Fig. 73 Conservación de la energía en el flujo de una alcantarilla.
|
|
-
Suponer V1 = 0, es decir, la velocidad es cero en el extremo aguas arriba.
-
Suponer V2 = 0, es decir,
la velocidad se disipa a cero en el extremo aguas abajo.
-
La pérdida de carga ∑hL es igual a la suma de las pérdidas
en la entrada (con coeficiente de pérdida Ke),
pérdidas en la salida (con coeficiente de pérdida
KE), y pérdidas a lo largo del conducto.
-
Usando la
ecuación de Darcy-Weisbach, la pérdida de carga es:
V 2
∑hL = [ (Ke + KE +
f (L / D ) ] _____
2g
| (188) |
-
De la Tabla 21, asumir
Ke = 0.5 y KE = 1 (Roberson et al., 1998).
| Tabla 21 Coeficientes de pérdida de carga en la
entrada, contracción, y expansión.
|
| Descripción |
Ilustración
(Hacer click en la figura
para mostrar) |
Datos adicionales |
Coeficiente de pérdida de cargaK |
| Entrada hL = Ke [V 2/(2g)] |
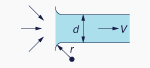
| r /d |
Ke |
| 0.0 |
0.50 |
| 0.1 |
0.12 |
| > 0.2 |
0.03 |
 |
|
1.0 |
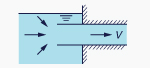
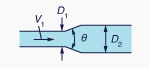
| Contracción hL = KC [V22/(2g)] |
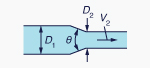 |
D2 /D1 |
KC
θ = 60° |
KC
θ = 180° |
| 0.0 |
0.08 | 0.50 |
| 0.2 |
0.08 | 0.49 |
| 0.4 |
0.07 | 0.42 |
| 0.6 |
0.06 | 0.32 |
| 0.8 |
0.05 | 0.18 |
| 0.9 |
0.04 | 0.10 |
| Expansión hL = KE [V12/(2g)] |
| D1 /D2 |
KE
θ = 10° |
KE
θ = 180° |
| 0.0 |
| 1.00 |
| 0.2 |
0.13 | 0.92 |
| 0.4 |
0.11 | 0.72 |
| 0.6 |
0.06 | 0.42 |
| 0.8 |
0.03 | 0.16 |
-
La relación entre el factor de fricción
de Darcy-Weisbach f y el n de Manning es
(Ponce, 2014):
8 g n 2
f = __________
k 2R 1/3
| (189) |
en la cual k = 1 en unidades SI, y k = 1.486 en las
unidades acostumbradas en EE.UU.
-
En las unidades acostumbradas en EE.UU., con k = 1.486, y g = 32.17 pies/s2:
116.55 n 2
f = ____________
R 1/3
| (190) |
-
Para un tubo circular: R = D / 4.
Por lo tanto:
185.01 n 2
f = ____________
D 1/3
| (191) |
-
De la Ec. 187, la conservación de la energía se reduce a:
z1 + y1 = z2 + y2 + ∑hL
| (192) |
La ecuación de pérdida de carga (Ec. 188) se repite
aquí por conveniencia:
V 2
∑hL = [ (Ke + KE +
f (L / D ) ] _____
2g
| (188) |
Reemplazando la Ec. 191 en la Ec. 188:
V 2
∑hL = [ 0.5 + 1.0 +
(185.01 n 2 L / D 4/3 ) ] _____
2g
| (194) |
Combinando las Ecs. 193 y 194:
V 2
6.5 = [ 1.5 +
(6.253 / D 4/3 ) ] _____
2g
| (195) |
-
La velocidad de flujo es: V = Q / A.
Por lo tanto: V = 200 / A = 200 / [ (π/4) D 2 ]
-
La carga de velocidad es: V 2 / (2g) = { 2002 / [ (π/4)2 D 4 ] } / (2g) = 1008 / D 4
-
Reemplazando la carga de velocidad en
la Ec. 195:
1008
6.5 = [ 1.5 +
(6.253 / D 4/3 ) ] _______
D 4
| (196) |
-
Resolviendo la Ec. 196 por iteración:
D = 4.38 pies. Para propósitos de diseño,
asumir el siguiente tamaño por exceso: D = 4.5 pies.
-
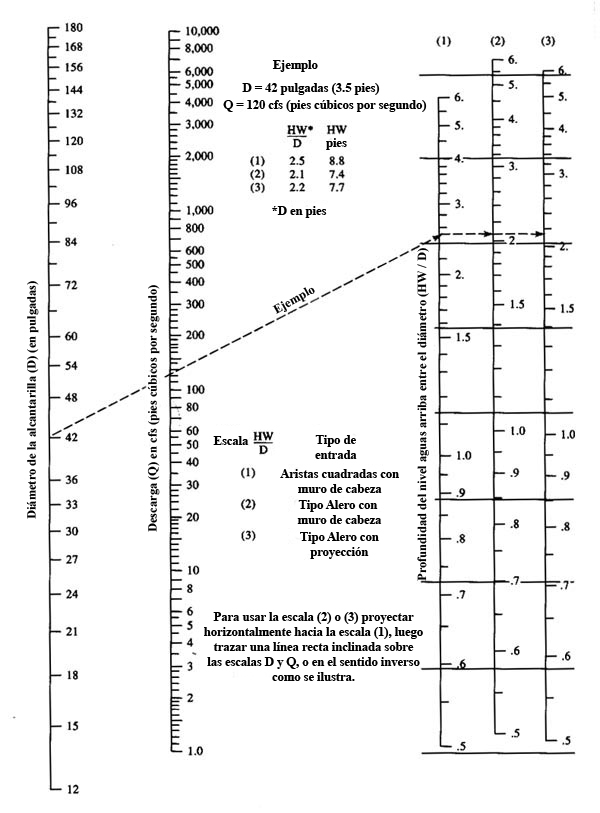
Con Q = 200 pies cúbicos por segundo, D = 4.5 ft = 54 pulgadas,
usar la Fig. 8-9 para encontrar la relación HW/D, es decir, la profundidad aguas arriba dividida entre el diámetro. En este caso: HW/D = 2.2, para una alcantarilla de
aristas cuadradas con muros de cabeza [Escala (1)].
|
Fig. 74 Relación profundidad
aguas arriba a diámetro (HW/D) para alcantarillas de concreto
y control en la entrada.
|
-
La profundidad aguas arriba es: HW = (HW/D) × D = 2.2 × 4.5 = 9.9 pies.
-
La elevación del nivel aguas arriba es: 100 + 9.9 = 109.9 pies. Esta elevación es mayor que
108 pies, lo cual es muy alto.
Por lo tanto el diámetro seleccionado D = 4.5 pies es demasiado pequeño.
Probar con el siguiente tamaño: D = 5 pies.
-
Con Q = 200 pies cúbicos por segundo, D = 5 pies = 60 pulgadas,
usar la Fig. 74 para encontrar la relación de la
profundidad aguas arriba dividida entre el diámetro
HW/D = 1.6, para el caso de aristas cuadradas con muros de cabeza [Escala (1)].
-
La profundidad del nivel aguas arriba es: HW = HW/D × D = 1.6 × 5 = 8 pies.
-
La elevación aguas arriba es:
100 + 8 = 108 pies. Esta elevación
es la misma que la de la elevación de
diseño; por lo tanto, el diseño está correcto.
-
Calcular la profundidad normal usando CANAL EN LÍNEA 06: yn = 3.284 pies.
-
Calcular la profundidad crítica usando CANAL EN LÍNEA 07: yc = 4.037 pies.
-
Dado que yn < yc,
el flujo es supercrítico.
-
Dado que TW = 3.5 > yn = 3.284, habrá un
pequeño salto hidráulico cerca de la salida.
-
El flujo es supercrítico a lo largo de gran parte
del conducto. Por lo tanto, se concluye que el control se encuentra en la entrada.
-
El diámetro de diseño es: D = 5 pies = 60 pulgadas. RESPUESTA.
|
Ejemplo No. 15A.
Usando
ENLÍNEA ALCANTARILLAS,
calcular el diámetro D de una alcantarilla circular de concreto,
con aristas cuadradas,
dadas las siguientes condiciones:
Descarga Q = 200 pies3/s;
elevación del fondo aguas arriba z1 = 100 pies;
coeficiente de Manning n = 0.013;
pendiente de fondo de la alcantariila So = 0.01;
profundidad aguas abajo y2 = 3,5 pies;
longitud de la alcantarilla L = 200 pies;
elevación de la rasante de la carretera Es = 110 pies;
bordo libre Fb = 2 pies;
coeficiente de pérdida en la entrada Ke = 0.5; y
coeficiente de pérdida en la salida KE = 1.0.
 | |
CÁLCULO EN LÍNEA. Los resultados de
ENLÍNEA ALCANTARILLAS
se muestran en la figura siguiente.
El diámetro de la alcantarilla es D = 5 pies.
|
|
[Haga click en la figura para desplegar]
|
Ejemplo No. 15B.
Usando
ENLÍNEA ALCANTARILLAS,
calcular el diámetro D de una alcantarilla circular de concreto,
con aristas cuadradas,
dadas las siguientes condiciones:
Descarga Q = 5.7 m3/s;
elevación del fondo aguas arriba z1 = 30 m;
coeficiente de Manning n = 0.013;
pendiente de fondo de la alcantariila So = 0.01;
profundidad aguas abajo y2 = 1.0 m;
longitud de la alcantarilla L = 60 m;
elevación de la rasante de la carretera Es = 33 m;
bordo libre Fb = 0.6 m;
coeficiente de pérdida en la entrada Ke = 0.5; y
coeficiente de pérdida en la salida KE = 1.0.
 | |
CÁLCULO EN LÍNEA. Los resultados de
ENLÍNEA ALCANTARILLAS
se muestran en la figura siguiente.
El diámetro de la alcantarilla es D = 1.524 m.
|
|
[Haga click en la figura para desplegar]
|
5. TRANSPORTE DE SEDIMENTOS
5.1 Naturaleza de los sedimentos
Todos las quebradas, corrientes y ríos que discurren sobre la superficie de la Tierra
acarrean materiales sólidos, tanto suspendidos como disueltos. A los
sólidos suspendidos
se los denomina sedimentos, y su transporte está
gobernado por leyes físicas; los sedimentos son las gravas, arenas, limos y arcillas.
Por el contrario, los materiales disueltos son
compuestos de tamaño molecular, lo cuales
están gobernados por leyes químicas.
Ejemplos de sólidos disueltos lo constituyen las sales, las cuales
están presentes, usualmente en concentraciones bajas, en las aguas de drenaje superficial.
El conocimiento del comportamiento de los sedimentos es importante en el
diseño y mantenimiento
de obras de drenaje de carreteras.
Todos los sedimentos tienen su origen en la roca madre,
la cual está constantemente sujeta a procesos de intemperismo. Una vez sueltos,
los sedimentos son eventualmente acarreados aguas abajo
por la capacidad erosiva de las
aguas de precipitación.
A mayor intensidad y altura de precipitación, mayor la fuerza erosiva y, por consiguiente,
mayor la cantidad de sedimentos acarreados.
La capacidad de transporte de sedimentos es un valor
que depende de variables hidráulicas tales como velocidad, profundidad, pendiente,
y tamaño del grano. Bajo flujo uniforme (sección prismática) o en equilibrio
(sección no prismática), la capacidad de transporte se calcula usando
fórmulas apropiadas (Sección 5.3). Cuando esta capacidad se reduce por cualquier motivo,
se produce la deposición de los sedimentos, lo cual puede llevar a problemas de drenaje.
Por ejemplo, la Fig. 75 muestra una alcantarilla parcialmente llena
de sedimentos. La Fig. 76 muestra un río efímero, cuya sección transversal
está parcialmente comprometida por la deposición de sedimentos.
|
Fig. 75 Alcantarilla sobre la Carretera 1, La Paz, Baja California, México.
|
|
Fig. 76 Puente sobre la carretera 1N (Panamericana), río La Leche, Lambayeque, Perú.
|
La ingeniería de sedimentos es la rama de la ingeniería
civil hidráulica
que trata de los sedimentos fluviales, incluyendo: (a) origen, (b) producción,
(c) transporte, (d) deposición, y (e) destino final.
Los sedimentos son producidos en sus orígenes,
en las cabeceras de las cuencas, y transportados
a través de la red fluvial hasta su eventual
deposición en los valles localizados aguas abajo, o su entrega directamente al
océano.
Una fracción de los sedimentos fluviales usualmente
llega hasta el océano, generalmente los granos más finos
(limos muy finos y arcillas).
La Fig. 77 (a) muestra un coluvión, una
deposición local de
sedimentos muy cerca a su origen, en las faldas de un cerro.
La Fig. 77 (b) muestra una quebrada o torrente, la cual, debido a su fuerte pendiente (So = 0.12), transporta
sedimentos de gran tamaño (cantos rodados).
|
Fig. 77 (a) Coluvión en la cabecera de la cuenca del río La Leche, Lambayeque, Perú.
|
|
Fig. 77 (b) Quebrada Rachichuela, cuenca del río La Leche, Lambayeque, Perú.
|
La ingeniería de
sedimentos comprende: (a) producción, (b) transporte, y (c) deposición.
La producción analiza los sedimentos
desde su origen en las cabeceras de las cuencas hasta su entrega
a las corrientes o ríos más cercanos. El transporte analiza los sedimentos
mientras permanecen en movimiento en las corrientes o ríos.
La deposición examina las cantidades o flujos
de sedimentos que dejan de ser transportados,
depositándose en algún
lugar de la cuenca (usualmente la cuenca baja), donde las pendientes hidráulicas o del terreno
disminuyen considerablemente.
En el drenaje de carreteras, la deposición de sedimentos
puede llegar a interferir con los flujos normales de drenaje, llevando en casos extremos a la falla del
sistema.
5.2 Producción y entrega de sedimentos
Todos los sedimentos son:
(a) producidos, (b) transportados, y (c) depositados en los valles y depresiones o, en su defecto,
entregados al océano más
cercano.
La producción de sedimentos es la suma total de todos los materiales
sólidos (cantos o bolones, grava, arena, limo, y arcilla), erosionados y removidos
de la cuenca que genera los sedimentos. La producción de sedimentos está
siempre referenciada al
área de la cuenca,
usualmente pequeña, y su correspondiente rendimiento,
el cual se mide en toneladas por hectárea.
Dado un punto A ubicado sobre el drenaje principal de
una cuenca, puede observarse que no todos los sedimentos
producidos aguas arriba llegan a dicho punto A, pues una fracción es siempre retenida
para formar parte de los valles. A la cantidad de sedimentos que llegan al punto A
se le denomina entrega de sedimentos.
En este caso, la ubicación del cálculo es en una sección transversal de la corriente, en la cual
se evalúan y/o miden los sedimentos que llegan hasta esa sección, en toneladas por día.
En el punto A, se denomina relación de entrega de sedimentos RES
a la relación (razón) entre los sedimentos entregados y los sedimentos producidos
(RES es siempre menor que 1, o en porcentage, menor que 100).
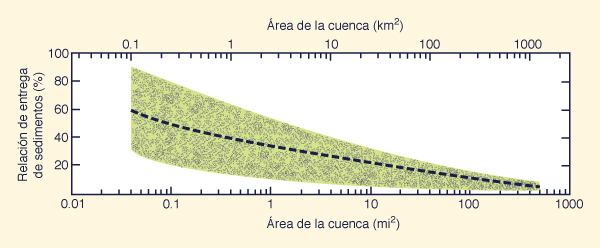
El valor de RES es una función del área de la cuenca, medida hasta el punto
de entrega (Fig. 78).
Puede observarse que el valor promedio de RES varía desde 60% para cuencas muy
pequeñas
(menores de 0.04 millas cuadradas, o 0.1 km2),
a 5% para cuencas grandes (mayores de 400 millas cuadradas, o 1000 km2).
|
Fig. 78 Diagrama típico de la relación de entrega de sedimentos (RES) vs área
de la cuenca.
|
5.2.1 Ecuación Universal de Pérdida de Suelo (EUPS)
La ecuación universal de pérdida de suelo (EUPS)
se utiliza para determinar
valores de producción de sedimentos, aplicable a parcelas agrícolas
o cuencas muy pequeñas, usualmente no mayores de algunas hectáreas (Wischmeier y Smith, 1965).
La ecuación es la siguiente:
en la cual A = pérdida anual de suelo
por erosión superficial, en toneladas por acre por año (1 acre = 0.405 ha);
R = factor de precipitación;
K = factor de erodibilidad del suelo;
L = factor de longitud;
S = factor de pendiente;
C = factor de manejo de cultivos; y
P = factor de la práctica de control de erosión.
Los factores de la Ec. 197 se pueden determinar consultando
un libro de ingeniería agrícola, hidrología, o sedimentos
(Ponce, 2014).
Cabe anotar que la Ec. 197 determina valores de producción de sedimentos, mas
no de entrega a un punto determinado, la cual es
siempre menor. La entrega de sedimentos disminuye conforme aumenta el tamaño de la cuenca;
véase la Fig. 78.
5.3 Transporte de sedimentos
La carga de sedimentos,
o descarga de sedimentos, usualmente referida como descarga sólida,
es la cantidad total de sedimentos transportados por una corriente o río
a través de una sección transversal dada, expresada en kilogramos/segundo
o Newtons/segundo.
De acuerdo al modo predominante
de transporte, la carga de sedimentos se divide
en: (1) carga de fondo, y (2) carga suspendida.
La carga de fondo es la fracción
que es transportada saltando y rodando sobre
el lecho, principalmente por acción de esfuerzos cortantes
causados por gradientes verticales de velocidad.
La carga suspendida es la fracción que es transportada en suspensión por acción de la turbulencia.
Cabe anotar que la carga de fondo consta de partículas
más gruesas que la carga suspendida.
Sin embargo, dependiendo de los esfuerzos cortantes locales, algunas partículas
se pueden mover como carga de fondo en un momento y como carga suspendida en otro.
De acuerdo a si las partículas están presentes en el lecho,
la carga de sedimentos
se divide en: (1) carga de material de fondo,
y (2) carga de material fino, comúnmente referida como
carga de lavado.
La carga de material de fondo es la fracción
cuyas partículas están presentes en el lecho en forma significativa;
por otro lado, la carga de lavado es la fracción
cuyas partículas no están presentes en el lecho.
En otras palabras, la carga de material de fondo es la fracción gruesa,
la cual es probable
que se haya originado en el lecho y que regrese a él bajo
condiciones apropriadas.
La carga de lavado es la fracción fina, la cual no proviene del lecho y
que no es probable que se deposite en él. Podría
decirse que la carga de material fino
es lavada a través del tramo de interés, y no depende de las condiciones hidráulicas del flujo (velocidad,
profundidad, y pendiente de fondo).
La Figura 79 muestra la relación entre las dos clasificaciones de descarga de sedimentos.
Se observa que los conceptos de carga de lavado y carga de fondo (color magenta claro y oscuro,
respectivamente) son mutuamente excluyentes.
La carga suspendida de material de fondo (color magenta intermedio) es la carga
en suspensión que proviene o está representada en el lecho.
Relación entre
las dos clasificaciones
de descarga de sedimentos |
Clasificación de acuerdo: |
| (1) Al modo predominante de transporte |
(2) A si las partículas están presentes en el lecho |
Carga total
de sedimentos | Carga de lavado |
Carga
suspendida | Carga
de lavado |
| Carga suspendida de material de fondo | Carga de material
de fondo |
| Carga de fondo | Carga de fondo |
Fig. 79 Relación entre las dos clasificaciones de descarga de sedimentos.
5.4 Fórmulas para el transporte de sedimentos
Los términos carga de sedimentos,
descarga de sedimentos, y descarga sólida
son sinónimos. Sin embargo, la carga de fondo, la carga suspendida de
material de fondo, y la carga de lavado son mutuamente excluyentes.
La predicción de transporte de sedimentos se refiere a la estimación
de la descarga de sedimentos en condiciones de equilibrio, es decir, bajo flujo permanente.
Existen varias fórmulas para la predicción del transporte de sedimentos.
La mayoría de las fórmulas calculan solamente la carga de material de fondo,
que consiste en: (a) carga de fondo y (b) carga suspendida de material de fondo (Fig. 79);
por ejemplo, las fórmulas de Duboys (Sección 5.4.1) y Colby (Sección 5.4.2).
El método de Einstein modificado (Sección 5.4.3)
calcula la carga total de sedimentos.
Todas las formulas existentes tienen componentes empíricos y, por lo tanto,
son aplicables principalmente dentro del rango de datos utilizados
en su desarrollo.
5.4.1 Fórmula de Duboys
La fórmula de Duboys es la siguiente:
qs = ψD τo ( τo - τc )
| (198) |
en la cual:
-
qs =
carga de material de fondo,
por unidad de ancho, en libras por segundo por pie;
ψD = parámetro de Duboys, el cual es función del tamaño medio
de las partículas, en pies cúbicos por libras por segundo;
τo = esfuerzo de cortante
en el lecho (fondo), en libras por pie cuadrado; y
τc =
esfuerzo cortante crítico, es decir, el esfuerzo cortante al inicio del movimiento, en libras por pie cuadrado.
La fórmula de Duboys es dimensionalmente homogénea.
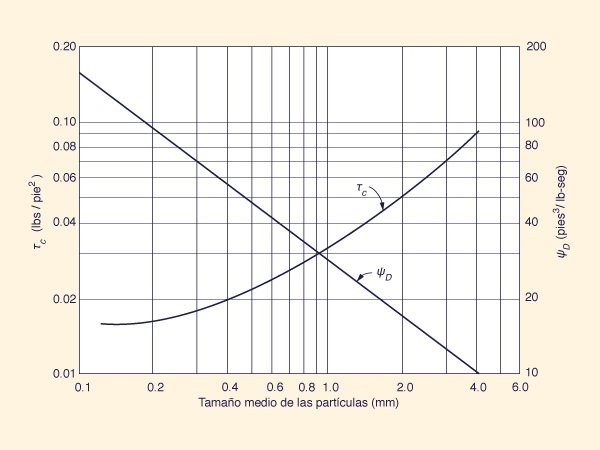
Los valores de ψD y τc
se obtienen de la Fig. 80.
|
Fig. 80 Valores de ψD y τc para
uso en la fórmula de Duboys [2].
|
Ejemplo 16A.
Dada una corriente de profundidad d = 12 pies, ancho b = 320 pies;
pendiente de fondo So = 0.0001, y tamaño medio de las partículas
d50 = 0.6 mm.
Calcular la carga de material de fondo en unidades acostumbradas en EE.UU. usando la fórmula de Duboys.
El esfuerzo cortante en el lecho es (Ponce, 2015):
τo = γ d So =
62.4 × 12 × 0.0001 = 0.07488 lb/pie2.
De la Fig. 80: ψD = 42 pies3/lb/s
De la Fig. 80:
τc = 0.025 lb/pies2
De la Ec. 198: qs = 42 × 0.07488 × (0.07488 - 0.025) = 0.157 lb/s/pie.
La carga de material de fondo es: Qs = qs b = 0.157 × 320 = 50.2 lb/s.
 | |
CÁLCULO EN LÍNEA.
Usando ENLINEA DUBOYS:
Qs = 50.551 lb/s, lo cual es equivalente a 2,183.821
toneladas/día.
|
|
|
Ejemplo 16B.
Dada una corriente de profundidad d = 3.658 m, ancho b = 97.54 m;
pendiente de fondo So = 0.0001, y tamaño medio de las partículas
d50 = 0.6 mm.
Calcular la carga de material de fondo en unidades SI (métricas) usando la fórmula de Duboys.
 | |
CÁLCULO EN LÍNEA.
Usando ENLINEA DUBOYS:
Qs = 22.937 kg/s, lo cual es equivalente a 1,981.782
toneladas métricas/día. Nótese que este resultado es equivalente al obtenido en el Ejemplo No. 16A.
|
|
|
5.4.2 Método de Colby
En 1964, Colby publicó un método para calcular la descarga de arena
en ríos de material de fondo predominantemente arenoso (Colby, 1964).
El desarrollo del método se basó en la formula de Einstein (1950), con el apoyo de grandes
cantidades de datos de laboratorio y de campo.
El método proporciona una predicción razonablemente buena de la carga de sedimentos, en particular para el caso de arenas.
El método requiere de los siguientes datos:
Velocidad media v,
Profundidad d,
Ancho B,
Temperatura del agua T,
Tamaño medio del sedimento d50, y
Concentración de la carga de lavado Cw.
El procedimiento es el siguiente:
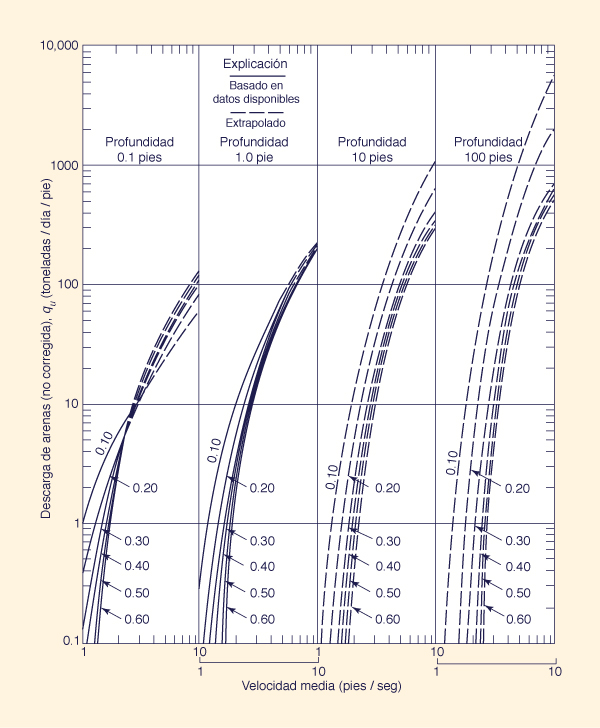
-
Calcular la descarga no corregida de
arena qu (en toneladas por día por pie)
en función de la velocidad media, profundidad, y tamaño medio del sedimento,
utilizando la Fig. 81.
|
Fig. 81 Descarga de arena en función de la velocidad media,
profundidad de flujo,
y tamaño medio del sedimento (Colby, 1964).
|
-
Para el caso de temperatura del agua T = 60 °F,
concentración de carga de lavado Cw baja (menos de 1000 ppm),
y tamaño medio del sedimento 0.2 ≤ d50
≤ 0.3 mm, no se requieren cálculos adicionales; qu
es de hecho la descarga de arena qs.
-
Para condiciones distintas a las anteriores, utilizar la
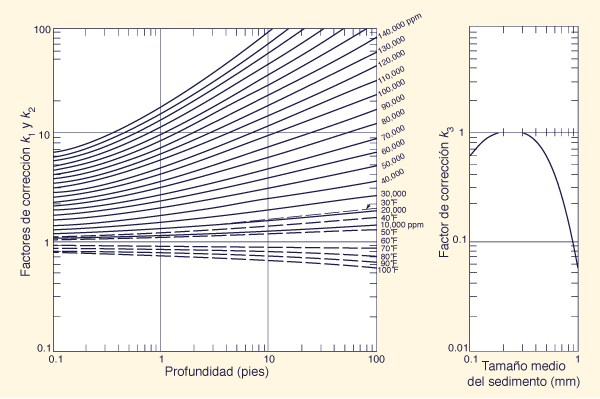
Fig. 82 para obtener los siguientes factores de corrección: (1) k1 en
función de la profundidad y temperatura del agua, (2) k2
en función de la profundidad y la concentración de la
carga de lavado, y (3) k3 en función del
tamaño medio del sedimento.
|
Fig. 82 Factores de corrección k1, k2, y
k3 en el método de Colby (1964).
|
-
La descarga de arena
se calcula utilizando la siguiente fórmula:
qs = [ 1 + (k1k2 - 1) k3 ] qu
| (199) |
en la cual qs = descarga de arena, en toneladas por día por pie.
Ejemplo 17A.
Dados: (1) velocidad media v = 2 pies/segundo, (2) profundidad d = 1 pie, (3) ancho de canal B = 30 pies, (4)
temperatura del agua 50 °F , (5) tamaño medio del sedimento d50 = 0.1 mm, y (6) concentración de la carga de lavado Cw
= 10 000 ppm. Calcular la descarga de arena por el método de Colby.
De la Fig. 81:
qu = 9 toneladas/día/pie.
De la Fig. 82:
k1 = 1.14, k2 = 1.22, k3 = 0.6.
De la Ec. 199:
qs = [ 1 + (1.14 × 1.22 - 1) × 0.6 ] × 9 = 11.11 toneladas/día/pie.
La descarga de arenas es: Qs = 11.11 × 30 = 333.3 toneladas/día.
 | |
CÁLCULO EN LÍNEA.
Usando ENLINEA COLBY,
la descarga de arenas es: Qs = 333.31 toneladas/día.
|
|
|
Ejemplo 17B.
Dados: (1) velocidad media v = 0.61 m/s, (2) profundidad d = 0.305 m, (3) ancho de canal B = 9.15 m,
(4) temperatura del agua 10 °C , (5) tamaño medio del sedimento d50 = 0.1 mm, y (6) concentración de la carga de lavado Cw
= 10 000 ppm. Calcular la descarga de arena por el método de Colby.
 | |
CÁLCULO EN LÍNEA.
Usando ENLINEA COLBY,
la descarga de arenas es: Qs = 303.15 toneladas métricas/día.
Nótese que este resultado es equivalente al obtenido en el Ejemplo No. 17A.
|
|
|
5.4.3 Método de Einstein Modificado
El método
de Einstein Modificado (MEM) fue desarrollado por
Colby y Hembree (1955) basado en el método de la carga de fondo (bed-load function) de Einstein (1950).
Cabe anotar que el método MEM es el único que calcula la carga total de sedimentos,
incluidas: (1) la carga de fondo, (2) la carga suspendida de material de fondo,
y (3) la carga de lavado (Fig. 79).
El método requiere de los siguientes muestreos:
Carga suspendida, la cual consiste de (véase la Fig. 79):
Material de fondo (material del lecho).
Las mediciones de carga suspendida no incluyen ni la carga de fondo ni
la fracción de carga suspendida que es transportada muy cerca del cauce,
las cuales son prácticamente imposibles de muestrear con precisión.
El MEM utiliza
el método de Einstein, conjuntamente con los datos de los muestreos de carga
suspendida y material de fondo,
para calcular la carga total de sedimentos, incluyendo la carga medida y la no medida.
Los datos requeridos
son las siguientes variables hidráulicas y sedimentológicas:
Descarga (líquida) Q,
Velocidad media u,
Profundidad (tirante) medio d,
Ancho (de la sección transversal) w,
Temperatura (del agua) T,
Diámetro de las partículas
D65 (65% por peso menor que este diámetro),
Diámetro de las partículas
D35 (35% por peso menor que este diámetro),
Concentración de sedimentos medida C,
Distancia vertical no muestreada dn, y
Profundidad media en las verticales muestreadas ds.
Adicionalmente, para cada tamaño de partícula
[nueve (9) para la forma corta, con sólo un tamaño de partículas finas;
o diez (10) para la forma larga,
con dos tamaños de partículas finas],
el método requiere de las fracciones de material de fondo ib
y el porcentaje de carga
suspendida Q's, obtenidas del análisis
granulométrico
de las muestras de material de fondo y carga suspendida, respectivamente.
La aplicación del método MEM se ilustra en los Ejemplos No. 18A y 18B.
Ejemplo 18A.
Dados los siguientes datos:
(1) descarga Q = 230 pies3/seg;
(2) velocidad media u = 2.08 pies/seg;
(3) profundidad media d = 0.98 pies;
(4) ancho w = 113 pies;
(5) temperatura = 64 °F;
(6) diámetro D65 = 0.00105 pies;
(7) diámetro D35 = 0.00075 pies;
(8) concentración de sedimentos medida C = 262 ppm;
(9) distancia vertical no muestreada dn = 0.3 pies; y
(10) profundidad media en las verticales muestreadas ds = 1.22 pies.
Las fracciones de material de fondo ib y porcentage de carga
suspendida Q's se muestran
en la Tabla 22.
Calcular la descarga total de sedimentos por el Método de Einstein Modificado (MEM).
Usar el modo de cálculo original (USBR, 1955).
Tabla 22 Fracciones de material de fondo
y porcentajes de carga suspendida. |
Tamaños de partícula
(mm) | ib | Q's
(%) |
| 0.002-0.0625 | 0.00 | 22 |
| 0.0625-0.125 | 0.00 | 25 |
| 0.125-0.25 | 0.38 | 42 |
| 0.25-0.5 | 0.50 | 11 |
| 0.5-1 | 0.05 | 0 |
| 1-2 | 0.01 | 0 |
| 2-4 | 0.01 | 0 |
| 4-8 | 0.00 | 0 |
| 8-16 | 0.00 | 0 |
 | |
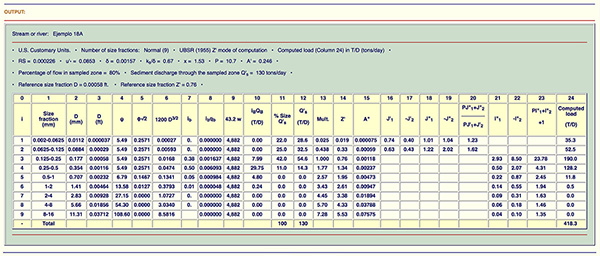
CÁLCULO EN LÍNEA.
Usando ONLINE MODIFIED EINSTEIN,
la descarga total de sedimentos es:
Qs = 418.3 toneladas/día (T/D).
Los cálculos se muestran en la figura siguiente.
|
|
[Haga click en la figura para desplegar]
Ejemplo 18B.
Dados los siguientes datos:
(1) descarga Q = 6.6 m3/s;
(2) velocidad media u = 0.63 m/s;
(3) profundidad media d = 0.3 m;
(4) ancho w = 34.4 m;
(5) temperatura = 18 °C;
(6) diámetro D65 = 0.32 mm;
(7) diámetro D35 = 0.23 mm;
(8) concentración de sedimentos medida C = 262 ppm;
(9) distancia vertical no muestreada dn = 0.09 m; y
(10) profundidad media en las verticales muestreadas ds = 0.37 m. Las fracciones de material de fondo ib y porcentage de carga
suspendida Q's se muestran
en la Tabla 22.
Calcular la descarga total de sedimentos por el Método de Einstein Modificado (MEM).
Usar el modo de cálculo original (USBR, 1955).
 | |
CÁLCULO EN LÍNEA.
Usando ONLINE MODIFIED EINSTEIN,
la descarga total de sedimentos es:
Qs = 375.4 toneladas métricas/día.
Los cálculos se muestran en la tabla adjunta. Nótese que los resultados son
equivalentes a los obtenidos en el Ejemplo No. 18A.
|
|
[Haga click en la figura para desplegar]
|
5.4.4 Otros métodos para el cálculo del transporte de sedimentos
Existen varias fórmulas para el cálculo del transporte de sedimentos. Las diversas fórmulas varían en su complejidad
y rango de aplicabilidad (Fig. 83).
Entre ellas se destacan las fórmulas de Engelund-Hansen, Ackers-White, y Einstein-Brown.
Para más detalles sobre éstas y otras fórmulas de
transporte de sedimentos, ver los manuales No. 54 (1975) y No. 110 (2008)
de la American Society of Civil Engineers (1975; 2008).
|
Fig. 83
Comparación entre varias fórmulas para el cálculo
del transporte de sedimentos
(Julien, 1995).
|
Ejemplo 19.
Dados: (1) velocidad media v = 1 m/s; (2) profundidad d = 1 m;
(3) ancho de la sección transversal (rectangular) B = 10 m, (4) pendiente S = 0.001;
(5) temperatura del agua T = 20 °C; y (6) tamaño medio del sedimento d50 = 0.1 mm. Calcular la descarga de sedimentos usando las siguientes fórmulas:
(1) Engelund-Hansen, (2) Ackers-White, y (3) Einstein-Brown. Usar las calculadoras
enlínea_calc.
 | |
CÁLCULO EN LÍNEA.
El perímetro mojado es P = 12 m.
El radio hidráulico es R = (10 × 1) /12 = 0.83 m.
La profundidad hidráulica es D = (10 × 1) /10 = 10 m.
Utilizando ENLINEA ENGELUND HANSEN,
la descarga de sedimentos es: Qs
= 1 545 toneladas métricas/día.
Utilizando ENLINEA ACKERS WHITE: Qs
= 10 195 toneladas métricas/día.
Utilizando ENLINEA EINSTEIN BROWN,
: Qs
= 9 779 toneladas métricas/día.
|
|
|
5.5 Curva de gasto de sedimentos
Una curva útil en el análisis de sedimentos es la curva de
gasto de sedimentos,
definida como la relación entre la descarga de agua y la descarga
de sedimentos en una sección transversal
dada.
La curva se obtiene mediante la medición simultánea de las descargas de agua y de sedimentos
o, en su defecto, indirectamente,
mediante el uso de fórmulas de transporte de sedimentos (véase la Fig. 83).
Para descargas pequeñas, la curva de gasto de sedimentos es usualmente
una línea recta en papel logarítmico, mostrando un aumento en la
concentración de sedimento con la descarga líquida.
Sin embargo, para descargas relativamente altas, la curva
tiene una tendencia asintótica a
una línea de igual concentración (isolínea)
(Fig. 84).
|
Fig. 84
Curva típica de gasto de sedimentos
(American Society of Civil Engineers, 1975).
|
Cabe hacer notar que la curva de gasto de sedimentos es estrictamente
válida sólo para condiciones de flujo permanente.
Bajo flujo no permanente, tanto las curvas de gasto de descarga líquida (la relación tirante-gasto) como las de
sedimentos son más elaboradas,
presentando fenómenos de histéresis y otras complejidades.
Estos fenómenos son intratables, y, por lo tanto, en la práctica
son normalmente despreciados.
6. PUENTES
6.1 Socavación de puentes
Los puentes son estructuras viales diseñadas con el fin de hacer posible el cruce
de un río o corriente por una carretera o camino. Los puentes
se diferencian de las alcantarillas (Sección 4) en su forma y usualmente mayor tamaño (Fig. 85). Generalmente, los puentes se
justifican en casos de cruces de carreteras con ríos importantes,
o cuando el volumen de
tráfico vehicular así lo requiera. En muchos casos, los estribos y/o pilares de los puentes
están colocados directamente sobre el cauce de los
ríos o corrientes (Fig. 86),
lo cual hace necesario un análisis de estabilidad.
|
Fig. 85 Puente sobre el río Sado, Alcaçer do Sal, Portugal.
|
|
Fig. 86 Puente sobre el río Kings, cerca de Stratford,
California, EE.UU.
|
El análisis de estabilidad comprende el estudio de socavación de uno o más pilares y/o estribos
de un
puente. Durante el paso de una avenida, el flujo se ve forzado a transitar por debajo del puente.
La presencia de uno o más pilares reduce la sección transversal efectiva de flujo; por lo tanto, las velocidades
aumentan y con esto, el flujo de sedimentos. Este proceso conduce eventualmente a la socavación (erosión)
del suelo alrededor del pilar, lo que, de ser de suficientemente magnitud, puede poner en peligro
la estabilidad de la superestructura y causar la falla eventual del puente.
La socavación es un fenómeno de flujo transitorio, el cual
se produce durante una avenida. El proceso es dual, caracterizado por:
(1) erosión durante la subida del hidrograma de avenida, y (2) deposición durante la bajada.
En muchos casos, el hoyo producido por la erosión durante la subida es rellenado por
la consiguiente deposición durante la bajada. La falla se produce cuando la profundidad del hoyo,
denominada profundidad de socavación, es de tal magnitud que compromete el nivel inferior
de cimentación
de la estructura. Por lo tanto, el objetivo del análisis es determinar la profundidad de socavación que
permita diseñar la cimentación del puente (en tipo, tamaño y profundidad) con un factor de seguridad adecuado.
6.2 Tipos de degradación, socavación, o erosión
La socavación, degradación, o erosión en las inmediaciones de la estructura de un puente puede deberse a uno o más de los siguientes
procesos:
Degradación general: La degradación relativamente lenta
del lecho fluvial, la cual obedece a fenómenos transitorios de transporte de sedimentos
en el río o corriente, actuantes en la macroescala longitudinal, más allá
del puente mismo;
Socavación por contracción: La erosión de la sección transversal natural de un
río,
causada por la contracción (es decir, la reducción de área de flujo)
impuesta por la presencia de los pilares o estribos del puente;
Socavación local: La erosión
rápida del lecho fluvial, durante un evento de avenida,
alrededor de los pilares o estribos de un puente;
Migración lateral: El cambio de alineamiento
del río en cuestión, el cual deja al puente en efecto fuera del curso establecido con
anterioridad a la migración.
La degradación general es causada por una reducción en la oferta de sedimentos en tramos
localizados aguas
arriba del punto de interés. Generalmente esto se debe a la degradación
inmediatamente aguas abajo de una represa, causada por el fenómeno de "agua hambrienta" (Fig. 87) (Lane, 1955),
o a la
extracción excesiva de áridos de los lechos fluviales vecinos (Fig. 88).
En algunos casos, la reducción en la oferta de sedimentos puede deberse
a cambios naturales o artificiales en el coeficiente de escurrimiento de la cuenca
localizada aguas arriba.
|
Fig. 87 Degradación debajo de la presa Fort Sumner, Río Pecos,
Nuevo México, EE.UU. (Lane, 1955).
|
|
Fig. 88 Degradación general por extracción de áridos, Arroyo Guadalupe, Baja California, México.
|
La socavación por contracción se manifiesta usualmente
a todo lo ancho del río,
durante el paso de una avenida extraordinaria (Fig. 89).
|
Fig. 89 Puente sobre el río Cuiaba, Mato Grosso, Brasil,
durante la avenida del 10 de enero de 1995.
|
La socavación local se produce por remoción de material de suelo
alrededor de los pilares, estribos, y otras estructuras de cimentación de los puentes,
causada por la aceleración del flujo en las vecindades y
la formación de vórtices inducidos por las obstrucciones
al flujo. La Figura 90 muestra
la falla de un puente de ferrocarril
cerca de Kingman, Arizona, ocurrida el 9 de agosto de 1997.
La falla del puente, la cual
llevó al descarrilamiento del ferrocarril, se debió
a la erosión y socavación
de los pilares y cimentación del puente, como resultado
de una avenida de período de retorno de 50 años
(National Transportation Safety Board, 1998).
|
,
Fig. 90 Falla por socavación debajo del puente de ferrocarril No.
504.1S, cerca de Kingman, Arizona.
|
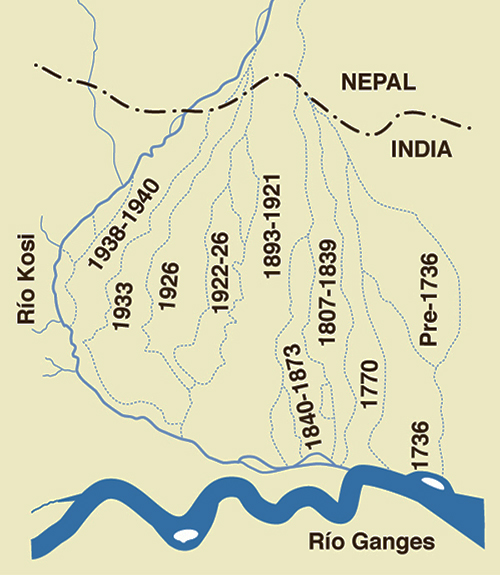
La migración lateral se produce cuando un río carga excesivas cantidades
de sedimento en situaciones geomorfológicas relativamente planas, lo cual lo obliga a rellenar su cauce y, por consiguiente,
a buscar nuevos rumbos, usualmente durante el paso de una avenida
extraordinaria (Fig. 91). En general, todo ensanchamiento o
desplazamiento lateral de un cauce fluvial pone en peligro la operatividad de un puente
colocado sobre él (Fig. 92). No parece haber una solución
simple a este problema de diseño.
|
Fig. 91 (a) Imagen satelital que muestra los
cambios de curso del río Kosi, en Bihar, India.
|
|
Fig. 91 (b) Cambios de curso del río Kosi, en Bihar, India, en los últimos
tres siglos.
|
|
Fig. 92 Puente abandonado sobre el río Piraí, Santa Cruz, Bolivia.
|
6.3 Socavación por contracción
La socavación por contracción ocurre cuando el área de flujo de una corriente es reducida ya sea: (a) por una contracción
natural, o (b) por una contracción artificial debida a la presencia de un puente.
En la mayoría de los casos, la socavación por contracción resulta en la profundización del
lecho del río.
La Figura 93 muestra el Pongo de Manseriche,
una contracción natural esculpida en roca, a través de la cual
el caudaloso río Marañón, uno de los dos grandes
ríos
que forman eventualmente
el río Amazonas,
ve reducido su ancho a 35 m, al descender los contrafuertes de
la Cordillera
Oriental de los Andes, en Amazonas, Perú.
El paso del pongo es particularmente peligroso por causa de los remolinos
que se forman debido a la extrema contracción del flujo,
como puede observarse en el video
Pongo de Manseriche.
|
Fig. 93 Sección mínima del Pongo de Manseriche, sobre
el río Marañon, Amazonas, Perú.
|
En ríos de lecho predominantemente arenoso,
existen dos tipos de socavación por contracción: (1) bajo agua clara, y (2) bajo lecho móvil.
La socavación por agua clara ocurre para números de Froude bajos, es decir, cuando la velocidad media es menor
que la velocidad crítica necesaria para el inicio del
movimiento (del lecho). En este caso
el área de flujo en la sección del puente, durante la avenida,
aumenta hasta que la velocidad media llega a ser igual a la crítica.
La socavación por lecho móvil ocurre para números de Froude más altos,
para los cuales la velocidad media es mayor que la
velocidad crítica necesaria para el inicio del movimiento del lecho.
En este caso
el área de flujo en la sección del puente, durante la avenida,
aumenta hasta que la cantidad
de material transportado que sale del volumen de control es igual
a la que entra.
Las fórmulas existentes para socavación por contracción requieren la determinación del tipo de socavación.
Para determinar si el flujo inmediatamente aguas arriba del puente está produciendo el movimiento del lecho,
es necesario calcular la velocidad crítica.
Con este fin, se puede usar la siguiente fórmula (U.S. Department of
Transportation, 2012, p. 6.2):
Vc = Ku y 1/6 D501/3
| (200) |
en la cual:
Vc = velocidad crítica necesaria para el inicio del movimiento del sedimento del lecho, en m/seg o pies/seg;
y = profundidad de flujo inmediatamente aguas arriba del puente, en m o pies;
D50 = diámetro medio de las partículas de sedimento del lecho ubicado inmediatamente aguas arriba del puente, en m o pies; y
Ku = constante empírica, igual a 6.19 en el sistema SI (métrico), y 11.17 en el sistema de unidades acostumbrado en los EE.UU.
Para obtener el D50 del material del lecho,
éste debe muestrearse en los primeros 0.3 m de profundidad. La Ec. 200 es aplicable a materiales granulares, estando restringida a valores
de D50 ≥ 0.0002 m (0.2 mm).
Para tamaños menores, la cohesión tiene el efecto de aumentar la velocidad crítica.
6.3.1 Geometría del diseño
El análisis de la socavación por contracción
depende de las condiciones geométricas particulares
del diseño.
Se pueden presentar los casos mostrados en las Figs. 94 y 95 (U.S. Department of Transportation, 2012):
1. Con flujo en la llanura de
inundación, la distancia entre los estribos es (Fig. 94):
Menor que el ancho del canal principal del río.
Igual al ancho del canal principal del río.
Mayor que el ancho del canal principal del río.
|
Fig. 94 (a) Socavación por contracción: Caso 1a.
|
|
Fig. 94 (b) Socavación por contracción: Caso 1b.
|
|
Fig. 94 (c) Socavación por contracción: Caso 1c.
|
2. Sin flujo en la llanura de
inundación, la sección del río es (Fig. 95):
|
Fig. 95 (a) Socavación por contracción: Caso 2a.
|
|
Fig. 95 (b) Socavación por contracción: Caso 2b.
|
6.3.2 Contracción bajo lecho móvil
La socavación por contracción bajo condiciones
de lecho móvil se calcula usando la ecuación modificada de Laursen (1960) (U.S. Department of Transportation, 2012, p. 6-10):
ys Q2 W1 yo
_____ = (____) 0.86 (____) k1 - ____
y1 Q1 W2 y1
| (201) |
en la cual:
ys = profundidad media de socavación por contracción bajo lecho móvil, en m o pies;
yo = profundidad media de flujo debajo del puente, antes de la socavación, en m o pies;
y1 = profundidad media inmediatamente aguas arriba del puente, en m o pies;
Q1 = flujo en la sección aguas arriba del puente, que transporta sedimento del lecho,
comprendiendo sólo el flujo en el canal principal, en m3/seg o pies3/seg;
Q2 = flujo en la
sección contraída, en m3/seg o pies3/seg;
W1 = ancho de fondo en la sección aguas arriba del puente, que transporta sedimento del lecho, en m o pies;
W2 = ancho de fondo en la sección contraída, que transporta sedimento del lecho, en m o pies;
k1 = exponente mostrado en la Tabla 23, en la cual:
V* = velocidad de corte inmediatamente
aguas arriba del puente = (g y1 S1 )1/2 ;
S1 = pendiente de la línea de energía en el canal principal; y
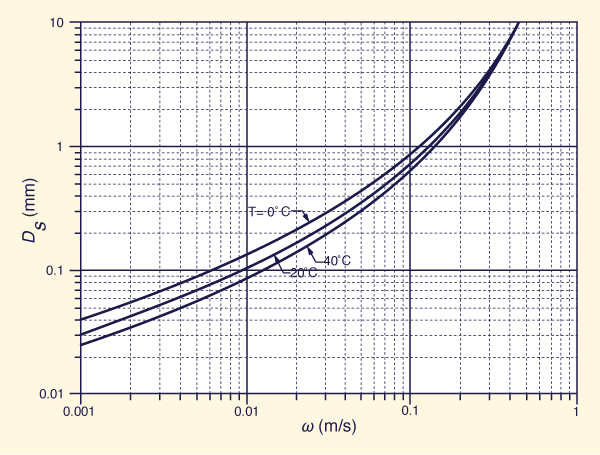
ω = velocidad de caída del sedimento, en función del diametro
Ds (Fig. 96), para el cual se toma el diámetro
medio D50.
| Tabla 23 Exponente k1 en la Ec. 201.
|
Relación
V* / ω |
Modo de transporte de la carga de sedimento |
k1 |
| < 0.5 |
Carga de fondo predominante | 0.59 |
| 0.5 - 2.0 |
Carga de fondo y alguna carga suspendida | 0.64 |
| > 2.0 |
Carga suspendida predominante | 0.69 |
|
Fig. 96 Velocidad de caída del sedimento.
|
Con referencia a la Ec. 201, cabe anotar lo siguiente:
Para los casos 1a y 1b, el valor de W2 es el flujo total a través
de la sección
contraída; sin embargo,
para el caso 1c,
la socavación por contracción debe calcularse separadamente: (a)
para el flujo de canal principal, (b) para el flujo de la llanura de inundación izquierda, y (c)
para el flujo de la llanura de inundación derecha.
En algunos casos, los valores de W1 y W2
no son fácilmente definibles; por lo tanto,
pueden ser reemplazados por los valores del ancho de la superficie de flujo, siempre y cuando
se usen ambos anchos ya sea
de fondo o de superficie. Sin embargo, el ancho
W2 normalmente se toma como el ancho de fondo,
excluyendo el ancho de el (los) pilar(es).
En lechos arenosos,
donde el hoyo o depresión producida por la contracción normalmente
se llena durante la recesión de la avenida,
puede aproximarse el valor de yo por el de y1.
Los sedimentos muy gruesos
pueden llevar al acorazamiento del lecho. En este caso, se recomienda
calcular la socavación por contracción por los dos métodos:
(a) lecho móvil, y (b) agua clara (ver la Sección 6.3.3).
El menor valor calculado debe ser usado para el diseño.
6.3.3 Contracción bajo agua clara
La socavación por contracción bajo condiciones
de agua clara se calcula usando la fórmula de Laursen (1963) (U.S. Department of Transportation, 2012, p. 6-12):
ys Ku
Q 2
_____ =
( ______________ ) 0.43 - 1
yo
Dm 0.67 W 2
| (202) |
en la cual:
ys = profundidad media de
socavación por contracción bajo agua clara, en m o pies;
yo = profundidad media del flujo debajo del puente, antes de la socavación, en m o pies;
W = ancho de fondo en la sección contraída, excluyendo
el ancho de los pilares, en m o pies;
Q = flujo en la
sección contraída, en m3/seg o pies3/seg;
Dm = diámetro
del menor tamaño de sedimento en la sección contraída,
que no es transportado, el cual se asume igual a
1.25 D50, en m o pies; y
Ku = constante empírica, igual a 0.025 en
unidades SI (métricas) y 0.0077 en unidades acostumbradas en EE.UU.
El valor mínimo de D50 a usar debe ser 0.0002 m (0.2 mm). Cabe notar que
el uso de un valor D50 < 0.2 mm resultará
en una sobreestimación de la socavación
por contracción bajo agua clara.
6.4 Socavación local
La socavación local es un de las causas más comunes
de falla de un puente por solicitación
hidráulica.
Los siguientes factores deben tomarse en cuenta
en el cálculo de la socavación local en un pilar o estribo:
Velocidad de flujo,
Profundidad de flujo,
Ancho del pilar,
Descarga interceptada
por el (los) estribo(s) y eventualmente regresada al canal principal,
Ángulo de
ataque del flujo de aguas arriba,
Longitud del pilar, si el pilar
está orientado
en ángulo respecto a la dirección predominante del flujo,
Tamaño y
distribución granulométrica del material del lecho,
La condición (configuración) del lecho, es decir,
las formas de fondo prevalecientes en el lecho, usualmente durante la avenida,
Forma de la sección
transversal del pilar o estribo,
Formación y/o transporte de hielo, y
Presencia de troncos y otra basura
transportada por el flujo.
La profundidad de socavación aumenta directamente con la velocidad y profundidad
de flujo. Por lo tanto, el riesgo de falla, usualmente
por causa de una profundidad de cimentación
insuficiente, aumenta en forma considerable durante
el paso de una avenida extraordinaria.
La profundidad de socavación no depende directamente
del tamaño del material del lecho. Sin embargo,
en el caso de materiales finos (limos y arcillas), la velocidad de
socavación es usualmente
más lenta
comparada con aquélla correspondiente a
los materiales gruesos (arenas).
Las fórmulas más establecidas para el cálculo
de la socavación local de pilares son las siguientes: (1)
HEC-18,
(2) Jain y Fisher,
(3) Froelich, y
(4) Melville. Estas fórmulas se detallan a continuación.
6.4.1 Fórmula HEC-18
La fórmula HEC-18 cálcula la máxima profundidad de socavación en lechos fluviales arenosos. La fórmula lleva su nombre de la publicación Hydraulic Engineering Circular No. 18
de la Administración Federal de Carreteras (FHWA),
del Departamento de Transportes de los EE.UU. (U.S.
Department of Transportation, 2012).
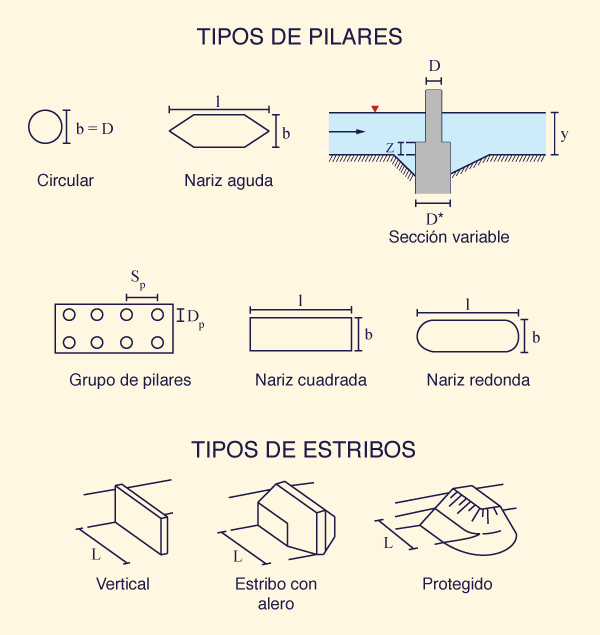
La fórmula HEC-18 es la siguiente (Fig. 97):
ys a
_____ = 2 K1 K2 K3 (____) 0.65 F 0.43
y1 y1
| (203) |
|
Fig. 97 Definición de variables en la socavación local de un pilar
de un puente.
|
en la cual:
ys = profundidad de socavación, en m;
y1 = profundidad de flujo inmediatamente aguas arriba del pilar, en m;
v1 = velocidad media del flujo inmediatamente aguas arriba del pilar, en m/s;
a = ancho del pilar, en m;
F = número de Froude = v1 / (gy1)1/2;
K1 = factor de corrección para tomar en cuenta la forma de la sección transversal (Fig. 98 y Tabla 24);
K2 = factor de corrección para tomar en cuenta el efecto del
ángulo θ entre el alineamiento del pilar y el alineamiento del flujo (el ángulo de ataque del flujo) (Ec. 204 o Tabla 25):
L
K2 = ( cos θ + ____ sin θ ) 0.65
a
| (204) |
en la cual
L = longitud del pilar, en m; y
θ = ángulo de ataque del pilar;
K3 = factor de corrección para tomar en cuenta la condición
del lecho fluvial (Tabla 26).
|
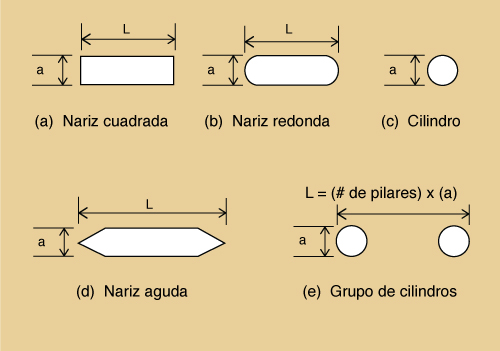
Fig. 98 Formas típicas de la sección transversal del pilar de un puente.
|
| Tabla 24 Factor de corrección K1.
|
| |
Forma de la sección transversal
(ver Fig. 96) |
K1 |
| a | Nariz cuadrada | 1.1 |
| b | Nariz redonda | 1.0 |
| c | Cilindro | 1.0 |
| d | Nariz aguda | 0.9 |
| e | Grupo de cilindros | 1.0 |
| Nota: Estos valores son válidos para ángulos de ataque θ ≤ 5°.
Para θ > 5°,
asumir K1 = 1. |
| Tabla 25 Factor de corrección K2.
|
Ángulo
de ataque
θ° |
L/a (ver L y a en la Fig. 96) |
4 |
8 |
12 |
| 0 | 1.0 |
1.0 | 1.0 |
| 15 | 1.5 |
2.0 | 2.5 |
| 30 | 2.0 |
2.75 | 3.5 |
| 45 | 2.3 |
3.3 | 4.3 |
| 90 | 2.5 |
3.9 | 5.0 |
| Nota: Estos valores son válidos
cuando toda la longitud L del pilar está sometida al ángulo de ataque θ. El valor máximo de K2 es 5. |
| Tabla 26 Factor de corrección K3.
|
| |
Condición del lecho fluvial | Altura de duna
H (m) |
K3 |
| a | Socavación con agua clara |
- | 1.1 |
| b | Lecho plano con antidunas |
- | 1.1 |
| c | Dunas pequeñas |
0.6 - 3 | 1.1 |
| d | Dunas medianas |
3 - 10 | 1.2 |
| e | Dunas grandes |
> 10 | 1.3 |
| Nota: Bajo frecuencias usuales de
diseño (el caso b), K3 = 1.1.
En presencia de dunas medianas a grandes (los casos d o e), el valor de K3 aumenta
como se indica. |
Ejemplo 20.
Dados: (1) profundidad y1 = 2 m;
(2) velocidad media v1 = 3 m/s;
(3) ancho del pilar a = 0.5 m;
(4) longitud del pilar L = 2 m;
(5) ángulo de ataque θ = 0°;
(6) sección transversal de nariz cuadrada; y
(7) lecho plano con antidunas.
Calcular la socavación local utilizando la formula HEC-18.
Para comprobación, utilizar
ONLINE SCOUR HEC-18.
 | |
CÁLCULO EN LÍNEA.
Utilizando las Ecs. 203 y 204, la profundidad de socavación local es:
ys = 1.66 m.
Utilizando
ONLINE SCOUR HEC-18: ys = 1.66 m.
|
|
|
6.4.2 Fórmula de Jain y Fisher
La fórmula de Jain y Fisher es aplicable al cálculo de la socavación local.
La fórmula distingue entre dos tipos de socavación:
Socavación bajo agua clara,
para números de Froude bajos, y
Socavación bajo lecho móvil, para números de Froude altos.
Las fórmulas son las siguientes:
a. Socavación bajo agua clara, para el caso (F - Fc ) ≤ 0.2:
ys y
_____ = 1.84 Fc 0.25 (____) 0.3
a a
| (205) |
b. Socavación bajo lecho móvil, para el caso (F - Fc ) > 0.2:
ys y
_____ = 2 (F - Fc ) 0.25 (____) 0.5
a a
| (206) |
en las cuales:
ys = profundidad de socavación;
a = ancho del pilar;
v = velocidad media del flujo inmediatamente aguas arriba;
y = profundidad del flujo inmediatamente aguas arriba;
Vc = velocidad crítica, al inicio del movimiento;
F = número de Froude = v/(gy)0.5; y
Fc = número de Froude crítico = Vc /(gy)0.5.
La velocidad crítica se puede estimar usando la
Ec. 200.
Ejemplo 21.
Dados:
(1) profundidad y = 2 m;
(2) velocidad media v = 3 m/s;
(3) ancho del pilar a = 0.5 m;
(4) diámetro medio de las particulas D50 = 1 mm.
Calcular la socavación local utilizando la formula de Jain y Fisher.
Para comprobación, utilizar
ONLINE SCOUR JAIN AND FISHER.
 | |
CÁLCULO EN LÍNEA.
Utilizando la Ec. 206, la profundidad de socavación local es:
ys = 1.698 m.
Utilizando
ONLINE SCOUR JAIN AND FISHER: ys = 1.698 m.
|
|
|
6.4.3 Fórmula de Froehlich
La fórmula de Froehlich es frecuentemente
usada para el cálculo de la socavación local
en el pilar de un puente (Fig. 99) (Froehlich, 1988).
La versión de la formula aplicable para
diseño es (Chase y Holnbeck, 2004):
ys be yo b
_____ = 0.32 φ (Fr1 ) 0.2 (____) 0.62 ( ____ ) 0.46 ( _____ ) 0.08 + 1
b b b D50
| (207) |
en la cual:
ys = profundidad de socavación (unidades L);
b = ancho del pilar (unidades L);
D50 = diámetro medio de las partículas (unidades L);
be = proyección del ancho del pilar b en un plano normal al ángulo de ataque θ (unidades L);
φ = coeficiente adimensional que toma en cuenta la forma de la sección transversal (ver Fig. 98): φ
= 1.3 para nariz cuadrada;
φ = 1.0 para nariz redondeada; y φ = 0.7 para nariz triangular.
v1 = velocidad media inmediatamente aguas arriba del pilar
(unidades L /T);
y1 = profundidad de flujo inmediatamente aguas arriba del pilar (unidades L);
Fr1 = número de Froude inmediatamente aguas arriba del pilar:
Fr1 = v1 /(gy1)0.5;
La Ec. 207 es adimensional cuando se usa con unidades de longitud consistentes (metros o piés).
|
Fig. 99 Detalle de un pilar del puente Petty Creek Road, sobre el río Clark,
cerca de Alberton, Montana, EE.UU. (Chase y Holnbeck, 2004).
|
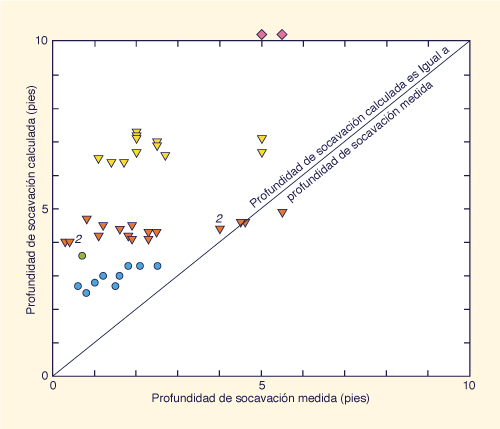
La Figura 100 muestra una evaluación de la Ec. 207.
Nótese que los valores calculados son casi siempre mayores
que los valores medidos. Asimismo, cabe notar que la fórmula de Froehlich es una de las incluídas en
HEC-RAS
(U.S. Army Corps of Engineers, 2016).
Ejemplo 22.
Dados:
(1) profundidad y = 2 m;
(2) velocidad media v = 3 m/s;
(3) ancho del pilar b = 0.5 m;
(4) ángulo de ataque del flujo θ = 0°;
(5) diámetro medio de las partículas D50 = 1 mm; y
(6) sección transversal de nariz cuadrada.
Calcular la socavación local aplicable para diseño utilizando la fórmula de Froehlich 1988.
Para comprobación, utilizar
ONLINE SCOUR FROEHLICH 1988.
 | |
CÁLCULO EN LÍNEA.
Utilizando la Ec. 207, la profundidad de socavación local es:
ys = 1.098 m.
Utilizando
ONLINE SCOUR FROEHLICH 1988: ys = 1.098 m.
|
|
|
6.4.4 Fórmula de Melville
La fórmula de Melville calcula la profundidad máxima de socavación
local en un pilar o estribo de un puente (Melville, 1997). La fórmula
está basada en un producto de seis variables empíricas K, cada una de las cuales
evalúa un factor
coadyuvante a la socavación local.
La fórmula es:
ds = KyW Ki
Kd Ks Kθ KG
| (208) |
en la cual:
ds = profundidad máxima de socavación local, en unidades de longitud (m o pies);
KyW = factor de profundidad: (a) Kyb para pilares, o (b) KyL para estribos,
en unidades de longitud (m o pies);
KI = factor de intensidad de flujo, el cual incluye efectos de la
gradación del sedimento y velocidad de flujo; adimensional;
Kd = factor de tamaño del sedimento; adimensional;
Ks = factor de forma del pilar o estribo; adimensional;
Kθ = factor de alineamiento del pilar o estribo; adimensional; y
KG = factor de geometría del canal; adimensional.
La Ecuación 206 evalúa la
socavación local de pilares o estribos en casos en los cuales
la socavación por contracción es despreciable.
Factor de profundidad del pilar o estribo
El factor de profundidad KyW (Kyb para pilares o
KyL para estribos) está
dado por una de las siguientes ecuaciones:
Kyb = 2.4 b
[para pilares angostos ⇒ (b /y ) ≤ 0.7]
| (209a) |
Kyb = 2 (yb )0.5
[para pilares intermedios ⇒ 0.7 < (b /y ) ≤ 5.0]
| (209b) |
Kyb = 4.5 y
[para pilares anchos ⇒ (b /y ) > 5.0]
| (209c) |
KyL = 2 L
[para estribos cortos ⇒ (L /y ) ≤ 1]
| (210a) |
KyL = 2 (yL )0.5
[para estribos intermedios ⇒ 1 < (L /y ) ≤ 25]
| (210b) |
KyL = 10 y
[para estribos largos ⇒ (L /y ) > 25]
| (210c) |
en las cuales:
y = profundidad de flujo inmediatamente aguas arriba del pilar o estribo;
b = ancho del pilar; y
L = longitud del estribo, incluyendo la aproximación del puente, proyectada en
dirección perpendicular al flujo.
Factor de intensidad de flujo
Respecto al factor de intensidad de flujo, es necesario distinguir
entre dos tipos de socavación local:
(1) bajo agua clara, y (2) bajo
lecho móvil, como en el caso de la fórmula de Jain y Fisher
(Sección 6.4.2). La socavación bajo agua clara ocurre antes del inicio
del movimiento del lecho, y la socavación bajo
lecho móvil después del inicio del movimiento.
La socavación bajo agua clara ocurre típicamente en el lecho
de la llanura de inundación. La socavación bajo lecho móvil ocurre
cuando hay transporte de sedimento en la vecindad del hoyo.
Si el sedimento es uniforme, es decir, con coeficiente de gradación
σg ≤ 1.3,
no se produce el acorazamiento del lecho. Contrariamente, si
el sedimento es no
uniforme, con coeficiente de gradación σg > 1.3,
sí se produce el acorazamiento del lecho, el cual
reduce efectivamente
la profundidad del hoyo [El coeficiente de gradación es: σg = (d84/d16)1/2].
El factor de intensidad de flujo KI está
dado por una de las siguientes ecuaciones:
KI = [V - (Va - Vc )] / Vc
{para [V - (Va - Vc )] / Vc < 1}
| (211a) |
KI = 1
{para [V - (Va - Vc )] / Vc ≥ 1}
| (211b) |
en las cuales:
V = velocidad media de flujo inmediatamente aguas arriba;
Vc = velocidad media del flujo inmediatamente aguas arriba,
al inicio del movimiento del lecho;
Va = velocidad media de flujo inmediatamente aguas arriba, al inicio
del flujo de lecho móvil (para sedimentos uniformes, Va = Vc;
para sedimentos no uniformes, Va > Vc);
Va = 0.8 Vca; y
Vca = velocidad media del flujo por encima de la cual
el sedimento de granulometría no uniforme
produce el acorazamiento del lecho.
Las velocidades Vc y Vca se calculan con las siguientes
fórmulas:
Vc
y
_____ = 5.75 log ( 5.53 _____ )
u*c
d50
| (212) |
Vca
y
______ = 5.75 log ( 5.53 ______ )
u*ca
d50a
| (213) |
en la cual:
d50 = diámetro medio de las partículas (mm);
d50a = dmax / 1.8; y
dmax = diámetro máximo de las partículas (mm).
Para sedimentos de cuarzo a la temperatura T = 20°C, las velocidades de corte u*c y u*ca se estiman con las siguientes
fórmulas:
u*c =
0.0115 + 0.0125 d501.4
[para 0.1 mm ≤ d50 < 1 mm]
| (214a) |
u*c =
0.0305 d500.5 - 0.0065 d50-1
[para 1 mm ≤ d50 < 100 mm]
| (214b) |
u*ca =
0.0115 + 0.0125 d50a1.4
[para 0.1 mm ≤ d50a < 1 mm]
| (215a) |
u*ca =
0.0305 d50a0.5 - 0.0065 d50a-1
[para 1 mm ≤ d50a < 100 mm]
| (215b) |
Factor de tamaño del sedimento
El factor de tamaño del sedimento Kd está
dado por una de las siguientes ecuaciones:
W
Kd = 0.57 log ( 2.24 _____ )
[para W /d50 ≤ 25]
d50
| (216a) |
Kd = 1
[para W /d50 > 25]
| (216b) |
en las cuales W = b para pilares, y W = L para estribos.
Factor de forma del pilar o estribo
El factor de forma Ks se muestra en la Tabla 27,
con referencia a la Fig. 101.
| Tabla 27 Factor de forma Ks .
|
| | |
Sección transversal
(ver la Fig. 101) |
Ks |
| Pilar | a | Cilindro circular | 1.0 |
| b | Nariz redonda | 1.0 |
| c | Nariz cuadrada | 1.1 |
| d | Nariz aguda | 0.9 |
| Estribo | a | Pared vertical | 1.0 |
| b | Pared de ala | 0.75 |
| c | Derrame a 0.5 H : 1 V | 0.6 |
| d | Derrame a 1 H : 1 V | 0.5 |
| e | Derrame a 1.5 H : 1 V | 0.45 |
Para estribos largos, el efecto de forma no es muy importante.
Por lo tanto, el factor Ks indicado en la Tabla 26
debe reemplazarse por el factor modificado K*s que sigue:
K*s = Ks
[para estribos cortos ⇒ (L / y ) ≤ 10 ]
| (217a) |
K*s = Ks + 0.667 (1 - Ks ) [ 0.1 (L/y ) - 1 ]
[para 10 < (L / y ) < 25 ]
| (217b) |
K*s = 1
[para estribos largos ⇒ (L / y ) ≥ 25 ]
| (217c) |
Factor de alineamiento del pilar o estribo
El factor de alineamiento Kθ está
dado por la Tabla 28. Cabe anotar que para el caso de pilares,
estos valores son iguales a los factores de corrección K1 mostrados en la Tabla 24.
| Tabla 28 Factor de alineamiento Kθ .
|
Ángulo
de ataque
θ° |
Kθ para pilares | Kθ
para
estribos |
L/a (ver L y a en la Fig. 96) |
4 |
8 |
12 |
| 0 | 1.0 |
1.0 | 1.0 | - |
| 15 | 1.5 |
2.0 | 2.5 | - |
| 30 | 2.0 |
2.75 | 3.5 | 0.9 |
| 45 | 2.3 |
3.3 | 4.3 | - |
| 60 | - |
- | - | 0.97 |
| 90 | 2.5 |
3.9 | 5.0 | 1.0 |
| 120 | - |
- | - | 1.06 |
| 150 | - |
- | - | 1.08 |
El factor Kθ para estribos
se aplica solamente para el caso de estribos largos.
Por lo tanto, este valor debe reemplazarse por el factor modificado K*θ que sigue:
K*θ = 1
[para estribos cortos ⇒ (L / y ) ≤ 1 ]
| (218a) |
K*θ = Kθ + (1 - Kθ ) [ 1.5 - 0.5 (L / y ) ]
[para 1 < (L / y ) < 3 ]
| (218b) |
K*θ = Kθ
[para estribos largos ⇒ (L / y ) ≥ 3 ]
| (218c) |
Factor de geometría del canal
En el caso de un pilar, la geometría del canal no influye
en la socavación. Por lo tanto, el factor de geometría
para un pilar es
KG = 1.
En el caso de un estribo, el factor KG está dado por la siguiente fórmula:
Estribo izquierdo
L*i y*i
n
KG = { 1 - ______
[ 1 - ( ____ ) 5/3 ____ ] } 1/2
Li y n*i
| (219a) |
en la cual (Fig. 102):
Li = longitud del estribo izquierdo;
L*i = ancho de la llanura de inundación del estribo izquierdo;
y = profundidad de flujo en el canal principal;
y*i = profundidad de flujo en la llanura de inundación del estribo izquierdo;
n = coeficiente de Manning en el canal principal; y
n*i = coeficiente de Manning en la llanura de inundación del estribo izquierdo.
Estribo derecho
L*r y*r
n
KG = { 1 - ______
[ 1 - ( ____ ) 5/3 ____ ] } 1/2
Lr y n*r
| (219b) |
en la cual (Fig. 102):
Lr = longitud del estribo derecho;
L*r = ancho de la llanura de inundación del estribo derecho;
y = profundidad de flujo en el canal principal;
y*r = profundidad de flujo en la llanura de inundación del estribo derecho;
n = coeficiente de Manning en el canal principal; y
n*r = coeficiente de Manning en la llanura de inundación del estribo derecho.
6.5 Cruces fluviales no convencionales
En la naturaleza,
los ríos se clasifican en: (1) perennes, (2) intermitentes, y (3) efímeros.
Los ríos perennes siempre tienen agua, la cual proviene del flujo de base [Fig. 103 (a)].
Los ríos intermitentes tienen agua solamente algunos meses al año, estando
los flujos de estiaje sostenidos por flujos estacionales de agua subterránea [Figs. 103 (b) y (c)].
Los ríos efímeros tienen agua solamente durante e inmediatamente
después de un evento de precipitación [Fig. 103 (d)].
La posición de la napa freática, encima, al nivel, o debajo del lecho del
río, determina si éste es perenne, intermitente, o efímero, respectivamente.
|
|
Fig. 103 (a) Arroyo Indio, California.
|
|
|
Fig. 102 (b) Río Gila, Arizona.
|
|
|
Fig. 102 (c) Arroyo Rosarito, Baja California.
|
|
|
Fig. 102 (d) Río Mojave, California.
|
|
La profundidad a la napa freática varía a través del espectro
climático, de las zonas áridas a las zonas húmedas.
En zonas húmedas, la napa freática está cercana a la superficie, mientras que en zonas áridas ésta se encuentra a profundidades mucho mayores.
En general, cuando más seco es el clima, mayor es la profundidad a la napa freática.
Por lo tanto, los ríos efímeros son bastante comunes en zonas áridas.
El pico de la erosión y el transporte de sedimentos
se produce alrededor de una precipitación media anual de 375 mm (15 pulgadas),
la cual corresponde a una zona árida
(200-400 mm) (Ponce et al., 2000) . Por lo tanto, los ríos ubicados
en zonas áridas usualmente transportan grandes cantidades de sedimentos.
Desde una perspectiva geomorfológica, cuando un río transporta
una gran cantidad de sedimentos, la relación
ancho-profundidad (es decir, la relación ancho-tirante) es grande, típicamente entre 50 y 100.
Por lo tanto, los cruces de ríos en zonas áridas representan un
desafío considerable para el diseño.
El problema es cómo posibilitar el cruce de un río efímero de una
manera efectiva y económica.
Los puentes fluviales pueden ser de varios tipos; en principio deben
cubrir todo el ancho del río (Fig. 104).
Cuando los puentes no cubren todo el ancho del río, esto lleva a problemas durante las avenidas.
Generalmente, durante una avenida el río reclama su ancho real, poniendo en peligro la cimentación y consecuente
estabilidad de la estructura.
Las velocidades excesivas en las inmediaciones de los pilares o estribos
pueden causar
erosión local y llevar a la eventual falla del puente.
|
Fig. 104 Puente Atirantado La Unidad, sobre el río Santa Catarina, Monterrey, Nuevo León,
México.
Este puente, en operación
desde 2003, resistió el embate del Huracán Alex
el 1 de julio de 2010.
|
Los puentes se contruyen cuando el tráfico o la importancia de la red vial justifica el costo.
La mayoría de los puentes son estructuras permanentes,
vulnerables a avenidas extremas.
Los ríos, particularmente aquéllos en zonas áridas, pueden rebalsar sus cauces o cambiar de curso,
haciendo inoperable la estructura de cruce (Fig. 92).
6.5.1 El badén o vado
Un baden o vado se define como un cruce, temporal o permanente,
de un río, arroyo, o corriente, sin el beneficio de un puente.
El badén constituye una alternativa de diseño
en casos de tráfico ligero o recursos limitados.
Los badenes construidos se diseñan para cruzar el río
sobre una loza de concreto, en los casos en los que
el flujo es pequeño o inexistente (Fig. 105).
En zonas áridas, los badenes son comunes en lugares donde el agua fluye solamente algunos días al año (Fig. 106).
Los badenes son una forma económica de resolver el problema del cruce de un río.
|
Fig. 105 Badén en Jaguaribira, sobre el río Jaguaribe, Ceará, Brasil.
|
|
Fig. 106 Badén sobre el Arroyo Guadalupe, Baja California, México.
|
La desventaja de un badén es que es posible que esté fuera de servicio algunos días al año, pero cuando esto se compara
con el costo de un puente, la decisión puede ser justificada.
Los badenes se usan generalmente
en áreas rurales, donde el tráfico y/o los recursos económicos
son limitados.
Un caso singular del cruce de un río importante mediante un badén construido
es el del Vado El Cora, el cual está diseñado
para operar sobre la presa derivadora El Jileño,
en el río Grande de Santiago, cerca de Tepic, Nayarit, México.
La longitud de la presa y badén
es de 473 m (Figs. 107 y 108).
El video Vado El Cora
describe esta inusual estructura.
|
Fig. 107 Vista aérea de la presa derivadora El Jileño,
Río Grande de Santiago, Nayarit, México.
|
|
Fig. 108 Cruce del Vado El Cora sobre la
presa derivadora El Jileño.
|
Durante avenidas extraordinarias,
los vados también están sujetos, como los puentes, a erosión hidráulica,
posible falla y consecuente inoperabilidad.
La Figura 109 muestra un badén en Indian Trail Road,
sobre el río Mojave,
cerca de Helendale, California: (a) durante la falla, en marzo de 2005, y (b) tres meses
después de la falla (junio 2005).
|
Fig. 109 (a) Badén en Indian Trial Road,
sobre el río Mojave, durante la avenida de marzo de 2005.
|
|
Fig. 109 (b) La intersección de Indian Trail Road con el río Mojave
en junio de 2005,
tres meses después
de la falla del badén.
|
6.5.2 El vado tipo Arizona
El vado tipo Arizona (Arizona crossing en Inglés) es un tipo de
vado usado en el sudoeste de los Estados Unidos para el cruce
de cauces fluviales efímeros. El vado consiste de un grupo
predeterminado de alcantarillas circulares, usualmente de aluminio corrugado,
alineadas formando un terraplén para posibilitar
el paso de vehículos por encima de éste (Fig. 110).
La longitud del terraplén usualmente comprende el cauce
principal del arroyo
o río. Este tipo de cruce está diseñado para un
rebalse limitado en caso de una avenida infrecuente o extraordinaria.
Existe la posibilidad de falla parcial o total
del terraplén como consecuencia de una
erosión hídrica excesiva.
|
Boys Scouts' Irvine Ranch
|
Fig. 110 El vado tipo Arizona, Condado de Orange, California.
|
El puente de alcantarillado (Fig. 111)
es similar al vado tipo Arizona. La diferencia
reside en que el puente de alcantarillado no está diseñado para
la eventualidad de un rebalse. Durante una avenida
extraordinaria, el rebalse usualmente pone en peligro la integridad
de la estructura.
|
Fig. 111 Puente de alcantarillado, Arroyo Tecate, Baja California,
México.
|
6.5.3 El vado-puente
Un vado-puente es una combinación de vado y puente,
con un máximo de las ventajas y un mínimo
de las desventajas.
El vado-puente está diseñado para trabajar como un puente durante el período
de estiaje y como un vado durante las avenidas.
En un río efímero, un vado-puente
se parece a un vado en su mayor parte,
pero contiene un puente relativamente pequeño, diseñado para pasar la avenida
media anual (Fig. 112).
|
Fig. 112 Esquema del vado-puente.
|
El vado-puente puede cubrir sin mayor costo el ancho total del río.
No hay necesidad de acortar el ancho de la estructura, y no hay pilares de puentes que puedan fallar durante una avenida extraordinaria.
Esencialmente, el vado-puente funciona como un vado
sólo durante las avenidas extraordinarias;
en otras ocasiones, el vado funciona como puente.
Por lo tanto, en ríos efímeros en zonas áridas,
el concepto de vado-puente ofrece una combinación apropiada de
funcionalidad
y economía.
Todos los cruces fluviales están diseñados para sostener
una carga hidrológica específica.
Ésta es usualmente la avenida de 100 años, y en ciertos
casos, aún mayores.
En un diseño típico de puente,
el caudal pico se expresa en términos
de las velocidades y tirantes, y estos datos
son utilizados para calcular
la socavación local en los pilares.
En contraste, un vado no tiene pilares;
el único requerimiento del diseño
es el anclaje apropiado de la losa para minimizar la
posibilidad de levantamiento.
Como en el caso de un puente, la posibilidad
de falla siempre existe durante solicitaciones extremas.
Los componentes de un vado-puente deben ser diseñados como vados y puentes, respectivamente.
El diseño del componente vado es del tipo convencional.
Sin embargo, el componente puente es
mucho menor que un puente típico.
El diseño del puente puede basarse en la avenida media anual,
es decir, la avenida de 2 años, la cual
desde un punto de vista geomorfológico es
formativa del canal principal del río.
Esto contrasta con la avenida de 100 años
usada en el diseño de puentes convencionales.
Durante eventos extremos, el vado distribuye
la carga hidráulica a través
de todo el ancho del río, sin mayores problemas.
Por lo tanto, el vado-puente está en mejores
condiciones de resistir el embate de las avenidas extraordinarias.
El vado-puente es una alternativa práctica
al puente o vado convencionales.
El concepto es aplicable en ríos efímeros con una gran
relación ancho-tirante,
particularmente en zonas rurales, o donde el tráfico
es ligero y los recursos económicos son limitados.
El diseño del vado-puente optimiza las
solicitaciones hidrológicas, utilizándose el puente
para las avenidas de 2 años y el vado para
las avenidas de 100 años.
Por lo tanto, el vado-puente es una solución
sostenible para cruces de ríos anchos
en zonas áridas predominantemente rurales.
6.6 Longevidad de un puente
En base a lo presentado en las Secciones 6.3 a 6.5,
puede concluirse que la longevidad de un puente depende de si su longitud
respeta la integridad hidráulica del río que cruza. Por ejemplo,
el puente romano sobre el río Guadiana, en Mérida,
España, el cual data
del Siglo 1 a.C.,
está todavía en operación (aunque
sólo en la modalidad peatonal),
habiendo sido parcialmente restaurado en varias ocasiones (Fig. 113).
Con 12 m de altura y una longitud
de 792 m en 60 arcos, el puente ocupa gran parte de la llanura de inundación
del caudaloso y regionalmente importante río Guadiana.
|
Fig. 113 Puente romano sobre el río Guadiana, Mérida, Extremadura,
España.
|
Otro ejemplo de longevidad lo constituye el llamado puente Inca, ubicado en las nacientes del
río Lauricocha, en Huánuco, Perú, para el cual se reporta
una antigüedad de más de 500 años.
La Figura 114 muestra claramente que este puente,
de 60 m de longitud y con un total de 24 vanos,
es aproximadamente seis (6) veces más largo que el ancho
del río durante el estiaje.
|
Fig. 114 Puente Inca ubicado en las nacientes del río Lauricocha, Huánuco, Perú.
|
BIBLIOGRAFÍA
American Society of Civil Engineers. 1975. Sedimentation Engineering, Manual No. 54.
American Society of Civil Engineers. 2008. Sedimentation Engineering: Processes, Measurements, Modeling and Practice, Manual No. 110.
Chase, K. J. y S. R. Holnbeck. 2004. Evaluation of pier-scour equations
for coarse-bed streams.
Scientific Investigations Report 2004-5111,
U.S. Dept. of Interior, U.S. Geological Survey, Reston, Virginia.
Chow, V. T. 1959. Open-channel Hydraulics. Mc-Graw Hill, New York.
Colby, B. R., y C. H. Hembree. 1955.
Computations of Total Sediment Discharge, Niobrara River Near Cody, Nebraska, U.S. Geological Survey Water-Supply Paper 1357, Washington, D.C.
Colby, B. R. 1964. "Discharge of Sands and Mean Velocity Relations in Sand-Bed Streams," U.S. Geological Survey Professional Paper 462-A, Washington, D.C.
Einstein, H. A. 1950.
The Bed-Load Function for Sediment Transportation in Open Channel Flows, USDA Soil Conservation Service, Technical Bulletin No. 1026, Washington, D.C., Septiembre.
Froehlich, D. C. 1988. Analysis of on-site measurements of
scour at piers,
in Abt, S.R., and Gessler, Johannes, eds.,
Proceedings of the 1988 National
Conference on Hydraulic Engineering, New York, American Society of Civil
Engineers, 534-539.
Julien, P. Y. 1995. Erosion and sedimentation. Cambridge University Press.
Lane, E. W. 1955. The importance of fluvial morphology in hydraulic engineering, Proceedings, ASCE,
Vol. 81, No. 745, Julio, 1-17.
Melville, B. W. 1997. Pier and abutment scour: Integrated approach, Journal of Hydraulic Engineering, ASCE,
Vol. 123, No. 2, Febrero, 125-136.
National Transportation Safety Board. 1998.
Railroad Accident Report:
Derailment of Amtrak Train 4, Southwest Chief,
on the Burlington Northern Santa Fe Railway near Kingman, Arizona, August 9, 1997,
PB98-916303 NTSB/RAR-98/03.
Ponce, V. M., R. P. Pandey, y S. Ercan. 2000. Characterization of drought across climatic spectrum,
Journal of Hydrologic Engineering, ASCE, Vol. 5, No. 2, Abril, 222-224.
Ponce, V. M. 2008. Preguntas y respuestas sobre el período de retorno a ser usado para diseño,
Artículo en línea.
Ponce, V. M. 2014. Engineering hydrology:
Principles and practices, Second edition, online.
Ponce, V. M. 2015. Fundamentos
de la Hidráulica de Canales, edición en línea.
Roberson, J. A., J. J. Cassidy, and M. H. Chaudhry. 1998. Hydraulic Engineering, Second edition, Wiley.
Wischmeier, W. H., y D. D. Smith. 1965. "Predicting Rainfall-Erosion Losses from Cropland East of the Rocky Mountains," USDA Agricultural Research Service, Agriculture Handbook No. 282, Mayo.
U.S. Army Corps of Engineers. 2016.
HEC-RAS River Analysis System, Hydraulic Reference Manual, Version 5.0, CDP-69, Febrero.
U.S. Department of Transportation. 2012. Evaluating Scour at Bridges, Hydraulic Engineering Circular No. 18, Fifth edition, Publication No. FHWA-HIF-12-003, Federal Highway Administration,
Abril.
|
http://ponce.sdsu.edu/drenaje_de_carreteras_b.html
|
180319 10:00
|
|
|